Может-ли ПО работать быстрее или взгляд изнутри

В наше время повсеместно используются компьютеры. Современный человек просто не представляет свою жизнь без компьютера. На сегодняшний день программные и технические средства ЭВМ развиваются очень быстро. Увеличивается скорость выполнения операций. В связи с этим многие пользователи и начинающие программисты считают, что с помощью современного компьютера можно «в лоб» решить любые задачи и, к сожалению, не задумываются, что при решении многих задач можно сэкономить как компьютерные, так и временные ресурсы. Конечно, при написании простых обывательских программ эти вопросы не актуальны. Но, когда речь заходит о таких серьезных отраслях как: криптография, архитектура, дизайнерские и графические приложения, то эти вопросы становятся очень актуальными и важными. Ведь при реализации этих приложений нужно проводить сложные математические вычисления. Важно, чтобы эти вычисления проходили быстро, так как таких вычислений нужно проводить очень много за малый промежуток времени. А в связи с этим важно, чтобы эти вычисления были реализованы оптимальным и экономичным способом.

by Cергей Апанасевич mjdel@tut.by
преподаватель информатики и математики

Эта статья и посвящена этим важным вопросам. В статье сразу рассказывается как на предварительном этапе, во время теоретической разработки ПО, можно подобрать оптимальное решение задачи и теоретически подсчитать экономию* компьютерного ресурса. Затем рассказывается, как во время написания кода программы можно выбрать или разработать более быстродействующую конструкцию.

Профилирование – сбор характеристик работы программы, таких как: время выполнения отдельных фрагментов (обычно подпрограмм), число верно предсказанных условных переходов, число кэш промахов и т.д. Характеристики могут быть аппаратными (время) или вызванные программным обеспечением (функциональный запрос). Инструментальные средства анализа программы чрезвычайно важны для того, чтобы понять поведение программы. Проектировщики ПО нуждаются в таких инструментальных средствах, чтобы оценить, как хорошо выполнена работа. Программисты нуждаются в инструментальных средствах, чтобы проанализировать их программы и идентифицировать критические участки программы.

Это часто используется, чтобы определить, как долго выполняются определенные части программы, как часто они выполняются, или генерировать граф вызовов (Call Graph). Обычно эта информация используется, чтобы идентифицировать те участки программы, которые работают больше всего. Эти трудоемкие участки могут быть оптимизированы, чтобы выполняться быстрее. Это – также общая методика для отладки.

Алгоритм Евклида

Рассмотрим алгоритм Евклида. Он был впервые изложен в одном из томов 13-ти томного сочинения Евклида (3 век до н.э.), известного под названием «Начла Евклида». Алгоритм нахождения наибольшего общего делителя двух натуральных чисел (НОД(a,b), где 0 < b <= a) базируется на теореме (1):

НОД(a,b)= НОД(b,r); (1)

где r – остаток от деления a на b. Известны ученые, такие как: Ламе, Гашков, Абрамов, Кормэн и другие, проводившие исследования, благодаря которым вывели формулы для предварительного расчета приблизительного количества шагов, за которое можно получить конечный результат. Рассмотрим эти формулы.

Французский математик Ж. Ламе в 1844 году доказал теорему о том, что число делений с остатком, необходимых для нахождения НОД двух натуральных чисел a и b, таких, что 0 < b <= a, не превышает пятикратного числа десятичных знаков наименьшего из этих двух чисел, т. е. m <=5p, где p – число разрядов числа b. Гашков предложил следующую формулу (2):

m<=[log?( (max(a,b)+1/2))]-1; (2)

где ?=(-1)/2, а m – искомое число. У Абрамова получилась такая формула (3):

m<=2[log2b]+2; (3)

Кормен подошел к этой проблеме с другой стороны. Пусть m – целое положительное число. Если 0<b<=a и b<=Fm+1, то результат будет достигнут не более чем за m шагов, где F – число Фибоначчи, m+1 – порядковый номер числа Фибоначчи.

Сейчас, для сравнения результатов, посмотрим рисунок 1 и 2. На рисунках изображена таблица, в которой сравнивается быстрота нахождения НОД-а двух чисел, при этом, в столбце «Реально», указано за сколько шагов находится НОД, а в столбцах «Ламэ», «Гашков», «Абрамов» и «Кормен» указаны результаты подсчета шагов для нахождения НОДа двух чисел по соответствующим формулам:

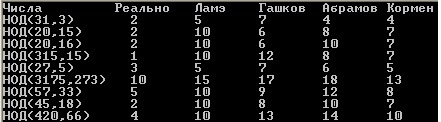
Рис. 1. Реальное нахождение НОДа двух чисел и теоретический расчет по формулам

На рисунке 2 отображены в виде графика значения из рисунка 1. Как показывает график, лучше всего работает формула Кормена. Конечно, для малых чисел эти формулы большой роли не играют, но, когда речь касается больших чисел, без них очень трудно обойтись. Это очень наглядно в криптографии при работе с алгоритмом RSA, где применяются числа с 20-ю и более разрядами.

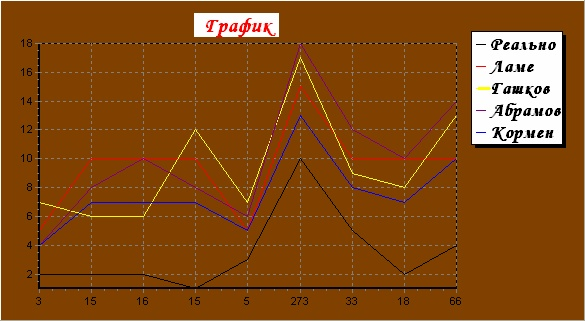
Рис. 2. Графическое изображение данных рисунка

Константа Капрекаса

А сейчас рассмотрим константу Капрекаса. Напомню, что это за константа. Задано четырехзначное натуральное число, у которого не все цифры равны между собой. Пусть a, b, c, d – четыре цифры десятичной записи этого числа. Получим из этих цифр два числа: в первом числе цифры расположены в порядке не возрастания, а во втором – в обратном порядке (неубывания). Вычтем из первого числа второе. К полученной разности применим туже процедуру.

Оказывается, что такое преобразование для любого начального элемента обязательно приведет через некоторое число шагов к числу 6174, которое и называется константой Капрекаса. Так вот, чтобы это доказать, можно пойти путем полного перебора. Для этого нужно рассмотреть все возможные варианты. Т.е. для всех четырехразрядных натуральных чисел не считая 1111, 2222, …, 9999 получим, что нужно проверить 8991 число. И не забывайте, что для каждого числа нужно несколько раз применить вышеописанную процедуру.

Попытаемся число вариантов перебора. Если a, b, c, d – цифры исходного числа и a>=b>=c>=d, то M1=1000a+100b+10c+d – наибольшее число из этих цифр, а M2=1000d+100c+10b+a – наименьшее число. Тогда их разность равна R=999(a-d)+90(b-c), где a>d, 0<a-d<=9, b-c<a-d. В итоге, нужно проверить 45 вариантов, что почти в 200 раз меньше, чем при полном переборе.

Интересно, а есть ли похожая константа для чисел с другим количеством цифр? Чтобы совершить проверку нужно предварительно найти предполагаемую константу. Для этого воспользуемся следующим правилом: если на двух последовательных шагах (операция описана при рассмотрении константы Капрекаса) получается одно и то же число, то это число и есть константа для данного n, где n – число разрядов проверяемого числа.

Рассмотрим n=3, т.е. 100, 101, 102, …, 988 – исходная последовательность за исключением 111, 222, …, 888. Компьютерная программа выдала следующий результат: искомое число равно 495. Если провести те же рассуждения, что и при сокращении вариантов перебора при константе Капрекаса, то получим 45 вариантов. Но, если рассмотреть оставшиеся числа окажется, что останется всего 5 вариантов, так как в остальных 40-ка числах повторяются одни и те же числа. А это почти в 180 раз меньше, чем при полном переборе. Если рассмотреть числа с количеством разрядов больше чем 4, то та же программа показывает, что константы нет, т.е. не выполняется начальное правило поиска константы.

Способы уменьшения временных затрат

А сейчас, давайте посмотрим, как во время написания кода можно еще больше уменьшить время выполнения программы. Многие программисты сталкиваются на этапе реализации программы с проблемой: какой из альтернативных процедур, функций или операторов воспользоваться. Например, как лучше возвести число х в квадрат: воспользоваться функцией Sqr(x) или х*х.

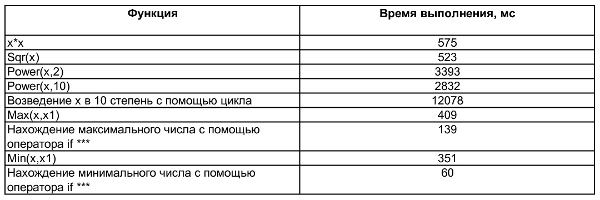
Часто выбор падает на более компактную конструкцию. И это объясняется тем, что так код программы легче читается и более краткий, а раз код меньше значит и программа выполняется быстрее. Вот тут и возникает вопрос: а будет ли более короткий код, выполнятся быстрее? Чтобы ответить на этот вопрос, рассмотрим таблицы 1 и 2**. В первой таблице сравниваются*** три цикла (цикл состоит из 100 млн. шагов). Во второй таблице сравниваются некоторые распространенные функции (результат получен на базе цикла for в 100 млн. шагов):

Табл.1. Сравнение трех циклов на быстродействие

Можно сказать, что циклы работают одинаково быстро****, и выбор конкретного цикла зависит в основном от условия решаемой задачи, т.е. для возведения числа х в квадрат лучше использовать функцию Sqr(x), которая почти в 1.1 раза быстрее работает, чем запись х*х, и в 6.5 раз быстрее, чем функция Power(x,2).

Если же нужно возвести число х в третью и большую степень, то, без сомнений, нужно воспользоваться функцией Power(), которая почти в 4.3 раза работает быстрее, чем возводить число х в нужную степень с помощью цикла. Также, предпочтительно, при нахождении максимального и минимального числа воспользоваться оператором if, который работает быстрее почти в 3 и 5.85 раз, чем соответствующие функции.

Табл.2. Сравнение распространенных операций на быстродействие

Можно конечно возразить, что для современных быстродействующих компьютеров это особо не влияет на скорость выполнения программы. Да, это так. Когда речь идет о выполнении учебных задач, то разница незаметна. Но когда речь идет о реальных программах и приложениях, малая экономия времени играет огромную роль. К примеру, в дизайнерских или архитектурных программах, где нужно за малое время обрабатывать огромное количество информации.

Или в криптографии, в частности, при использовании алгоритма RSA, где приходится оперировать простыми числами с двадцатью и более разрядами.

Сейчас подведем итоги

Во-первых, мы убедились в том, что вопросы увеличения производительности программ и экономия компьютерного ресурса очень важны и актуальны.

Во-вторых, мы убедились в том, что начинать экономить ресурсы компьютера и увеличивать производительность ПО можно на этапе теоретической разработки приложения.

В-третьих, при написании кода программ, если сделать «правильный выбор», также можно увеличить производительность ПО.

В-четвертых, когда пишется программа, нужно осознанно выбирать те или иные операторы, учитывая, в первую очередь, какие из них выполняются быстрее, и только потом на краткость записи кода. Ведь код всегда можно читабельно оформить. И не забывайте, что код программы будут видеть только единицы, а пользоваться продуктом множество людей, далеко не программистов. Их будет мало интересовать, как записан код. Главное, чтобы программа работала быстро и надежно.

Статья из седьмого выпуска журнала «ПРОграммист».