Применение изометрических координат в Delphi

Posted by bullvinkle under Журнал, Статьи

В данной статье рассмотрены методы применения изометрии на канве. Позволяет получить псевдо-эффект 3D на двухмерной плоскости.

Автор: Владимир Дегтярь aka DeKot degvv@mail.ru

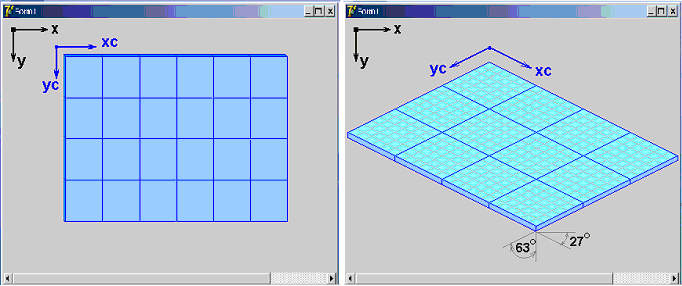
Рис. 1 Игровое поле в прямоугольных  и изометрических координатах.

1. Построение изометрической матрицы

При создании простых 2D игр (аркады, «стрелялки» и т.п.) обычно для построения игрового поля  используется двухмерная  матрица с координатами, привязанными к координатам экрана (формы). При этом, направления координат игрового поля  и экрана совпадают, и плоскость поля располагается как бы вертикально перед пользователем. Некоторую  объемность изображения и эффект перспективы, правда, можно получить за счет манипулирования масштабом графических элементов. Но все это достигается  путем значительного усложнения кода программы и требует сложных математических вычислений.

Значительно лучший визуальный эффект можно получить при применении изометрических координат для игрового поля. В этом случае поле для пользователя как бы наклонено под определенными углами по отношению к плоскости, а значит и координатам, экрана. При применении матрицы в изометрических координатах требуется привести координаты ячеек поля  и индексы  массивов, описывающих такую матрицу к прямоугольным координатам экрана. Для случая, когда матрица игрового поля выполнена в изометрических координатах, можно применить следующие функции для определения индексов массива по координатам формы или же  координаты ячеек массива по индексам. Необходимые данные приведены на рисунке 2:

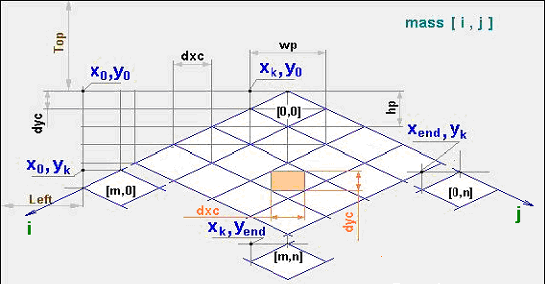
Рис. 2 Необходимые данные.

Думаю понятно, что (см. листинг 1):

ЛИСТИНГ-1

…

mas: array [ 0..m,0..n ] of  < тип данных >,

где  i — в диапазоне 0 .. m, j — в диапазоне 0..n;

Left, Top – смещение от края формы;

dxc, dyc – шаг координат ячеек матрицы;

dxc := 2 * dyc;

wp, hp – ширина и высота ячейки матрицы в координатах формы;

wp := 2 * dxc;  hp := 2 * dyc;

x0 = Left;  y0 = Top;

Для определения координат ячейки по индексам (см. листинг 2):

ЛИСТИНГ-2

…

function Kord_X(i , j : byte) : integer;

begin

Result:= ((m + ( j – i)) * dxc ) + Left

end ;

x := Kord_X(i , j);

function Kord_Y(i , j : byte) : integer;

begin

Result := ((i + j) * dyc) + Top

end;

y := Kord_Y(i , j);

Для определения индексов по координатам (см. листинг 3):

ЛИСТИНГ-3

…

function Ind_I (x , y : integer) : integer;

begin

Result := ((m – ((x – Left) div dxc)) + ((y -Top) div dyc)) div 2

end;

i := Ind_I (x , y);

function Ind_J (x , y : integer) : integer;

begin

Result := (((x -Left) div dxc) + (((y -Top) div dyc) – m)) div 2

end;

j := Ind_J (x , y);

При определении координат по курсору мыши , необходимо  назначить область “чувствительности” курсора в пределах области , показанной на рисунке оранжевым цветом. Тогда координаты  x , y  ячейки матрицы по координатам курсора xm , ym определяются следующим образом (см. листинг 4):

ЛИСТИНГ-4

…

procedure TForm1.FormMouseUp (Sender : TObject ; Button : TMouseButton ;

Shift : TShiftState ; xm , ym : Integer) ;

begin

x := ((((xm – Left) + (dxc div 2)) div dxc) * dxc) + Left;

y := ((((ym – Top) + (dyc div 2)) div dyc) * dyc) + Top

end;

2. Графические объекты в изометрических координатах

Для удобства работы с графикой в изометрических координатах следует тщательно подходить к соотношениям размеров объектов и размерами ячеек матрицы. Так, углы расположения матрицы – 27?  и 63?  указаны не  случайно. При работе с пиксельными изображениями форматов BMP, JPG, PNG и аналогичных этот наклон наиболее удобен для отображения различных элементов.

Для движущихся объектов, реализуемых в виде отдельных рисунков или спрайтов следует применять следующие пропорции в  размерах: Sprite.Width:= 1 / 3 * wp;  Sprite.Height:= 2 / 3 * hp или Sprite.Width:= 2 / 3 * wp;  Sprite.Height:= hp.

Здесь: wp и hp — соответственно  ширина и высота ячейки матрицы (см. рис.3).

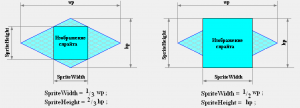
Рис.3 Организация движения спрайта.

При организации движения спрайта приращения по координатам dx и dy должны иметь соотношение 2:1 и  соответствовать условию:

N_step =  dxc / dx,  или N_step = dyc  / dy;

Где  N_step  —  количество приращений за один такт (шаг) в цикле или по таймеру ;

dxc , dyc  —  шаг  координат ячеек изометрической матрицы ;

Приведем пример (см. листинг 5):

ЛИСТИНГ-5

…

for i:= 1 to N_step do begin

Sprite(x,y) ; // процедура вывода спрайта на форму в  координатах  x , y;

x := x + dx ;  y := y + dy ;

end;

При выполнении такого условия координаты спрайта всегда после выполнения шага движения  попадают в координаты следующей ячейки. При использовании обработчика нажатия клавиш «cтрелки» приращения координат спрайта принимают следующие значения (см. рис.4):

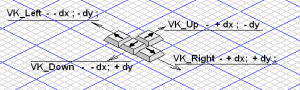
Рис. 4. Приращение координат спрайта

3. Многомерная матрица игрового поля в изометрических координатах.

До сих пор мы рассматривали двухмерную изометрическую матрицу, расположенную в одной плоскости.  Для получения реального трехмерного изображения можно применять многомерную матрицу в  трех изометрических координатах (см. рис.5):

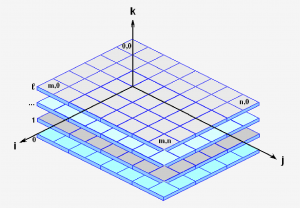
Рис. 5. Отображение многомерной матрицы в изометрических координатах

Такая  матрица описывается следующим массивом (см. листинг 6):

ЛИСТИНГ-6

…

mas_index : array [ 0 .. l , 0 .. m , 0 .. n ] of < тип данных >  или…

mas_index [ k , I , j ] ;   здесь индекс k находится в  диапазоне значений 0..l;

i   —  0..m;

j   —  0..n;

Работа с такой матрицей в пределах одного слоя  аналогична  описанию в разделе 1 в соответствии с рисунком 1. Однако при переходе с одного уровня  на другой следует учитывать следующие особенности:

• каждый последующий слой в экранных  прямоугольных координатах сдвигается на величину dyc
• при организации движения графических объектов приращения координат объекта в экранных

координатах  задаются одинаковыми dx := dy и выполняется условие dx * N_step = dxc

В этом случае, при переходах между уровнями (при использовании обработчика клавиш «стрелки») изменения индексов ячеек  матрицы следующие (см. таблицу и рисунок 6):

Таблица. Изменения индексов ячеек матрицы

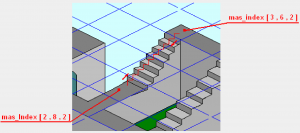
Рис. 6. Визуализация переходов

Далее, после перехода на следующий уровень обработка кода происходит как с двухмерной матрицей с учетом новых индексов в массиве индексов.

Заключение

Пример применения многомерной изометрической матрицы приведен в ресурсах к статье на http://www.programmersforum.ru в разделе «Журнал клуба программистов. Первый выпуск». В следующих уроках мы научимся работать с графикой на канве в среде Дельфи

Статья из первого выпуска “журнала ПРОграммистов”.
Скачать этот номер можно по ссылке.
Ознакомиться со всеми номерами журнала.

Обсудить на форуме — Применение изометрических координат в Delphi

Похожие статьи

• Делаем динамические тени на OPENGL. Часть 1
• Как работать с графикой на канве в среде Дельфи. Урок 7-8
• Анимация в WEB на JavaScript
• GAMEDEV на Delphi. Делаем змейку
• 3D НЕБО в DELPHI
• Как работать с графикой на канве в среде Дельфи
• Как работать с графикой на канве в среде Дельфи. Урок 1–2
• Заливка замкнутого контура, как в Paint
• Рисование эллипса удержанием кнопки на любом месте TImage
• Вращение шестиугольника в Делфи 7