Немного о DSP. Часть 2

В школе нам говорили, что если дискриминант D квадратного уравнения меньше нуля, то оно не имеет решений. В принципе, верно, но только отчасти. Решений нет среди вещественных чисел. Но они есть (их даже два) среди комплексных чисел. Между прочим, комплексные числа как раз и придумали для того, чтобы любое алгебраическое уравнение имело решения.

Тут будет немного математики. Комплексное число определяется как упорядоченная пара вида (a,b), где a,b – вещественные, a – называется вещественной частью, b – мнимой. Комплексные числа можно складывать и умножать по следующим правилам:

(a, b) + (c, d) = (a + c, b + d)
(a, b)(c, d) = (ac + bd, ad + bc)

Одним из замечательных свойств комплексных чисел является то, что если второе число в паре равно 0, то числа вида (a, 0) складываются и умножаются как обычные вещественные (предлагаю это проверить). Поэтому все вещественные числа можно считать комплексными с нулевой мнимой частью: a = (a, 0).

Но с какими-то абстрактными парами оперировать неудобно, да еще надо помнить правило умножения. Оказывается, что комплексные числа можно представить в таком виде: (a,b) = a + i*b, где i — это специальное число, называемое мнимой единицей, i = (0, 1). В таком виде можно легко оперировать комплексными числами, используя сложение и умножение так, как мы привыкли в алгебре (раскрывая скобки и группируя подобные). Кстати, если умножить i на i, получится -1: (0, 1) * (0, 1) = (-1, 0).

Можно проверить, что операции сложения и умножения при таком представлении остаются справедливыми:

(a + ib) + (c + id) = (a + c) + i(b + d)
(a + ib) * (c + id) = ac + ibc + iad + i²db

= { вспоминая, что i*i = -1 } =

(ac — db) + i(ad + bc)

Иногда удобно представлять комплексные числа как векторы на плоскости с соответствующими координатами. Тогда операция сложения естественным образом сведется к сложению векторов.

Ну и вот пример уравнения, имеющего комплексные решения:

x² + 1 = 0

Решениями являются:

x₁ = -i, x₂ = i

В реальной жизни довольно трудно встретить комплексное число. Например, нельзя что-то измерить и получить мнимое значение. Все физические величины, с которыми мы имеем дело в повседневной жизни, вещественны (масса, сила, давление, скорость и т.д.). Но комплексные числа очень удобны для описания некоторых процессов в физике, например колебаний, и вот почему.

Для комплексных чисел существует еще одно представление, тригонометрическое. Вспомним, что комплексные числа можно расположить на плоскости. Введя на этой плоскости полярную систему координат, практически сразу получим и тригонометрическое представление:

(a, b) = a + ib =

заменяя:

a = r cos(t), b = r sin(t) = r(cos(t) + i sin(t))

Другими словами, вектор на плоскости (комплексное число) можно представить как два числа t, r- азимут и расстояние до точки. называется аргументом, а r- модулем комплексного числа. Теперь перепишем в тригонометрическом представлении операцию умножения. Пусть даны два числа:

(a, b) = r1(cos(t₁) + i sin(t₁))
(c, d) = r2(cos(t₂) + i sin(t₂))

тогда:

(a, b)(c, d) = r₁(cos(t₁) + i sin(t₁))r₂(cos(t₂) + i sin(t₂)) == r₁r₂(cos(t₁)cos(t₂) — sin(t₁)sin(t₂ + i(cos(t₁)sin(t₂) + cos(t₂)sin(t₁))) =
= { применяя формулы приведения для синуса суммы и косинуса суммы } =
= r₁r₂(cos(t₁ + t₂) + i sin(t₁ + t₂))

Другими словами, при умножении двух комплексных чисел модули перемножаются, а аргументы — складываются. Причем, если оба комплексных числа имели модуль 1, то перемножение их — это просто поворот единичного вектора (первого числа) вокруг нуля на угол, равный аргументу второго числа. Или наоборот, числа можно поменять ролями. А вещественные числа – это векторы, лежащие на оси Ox.

Еще одна вещь, которая нам понадобится формула Эйлера:

e^it = cos(t) + i sin(t)

Из этой формулы получаем, что любое комплексное число:

z = r(cos(t) + i sin(t))

можно представить так:

z = r * e^it

Отсюда делаем вывод, что любое комплексное число — это обычное положительное вещественное число r, повернутое на угол t умножением на e^it.

И вот пример. Вспомним из школьной физики, что положение маятника можно описать такой формулой:

x = A cos(ωt + φ₀)
где:  φ₀ — начальная фаза;  ω — угловая скорость;   А — амплитуда.

Рассмотрим комплексное число:

q = q₀e^iωt
где:  q₀ = Ae^iφ₀

Если взять вещественную часть от q, то как раз получим наше положение маятника x. Чем же это удобно? А тем, что при такой записи q = q₀e^iωt  описание колебаний маятника сводится к простому умножению одного комплексного числа (q₀) на другое (e^iωt).

В более сложных теориях оперировать комплексными числами намного удобнее. Вот одним из таких примеров и будет преобразование Фурье.

Преобразование Фурье

Как известно, современный цифровой компьютер — устройство сугубо дисретное, и работает компьютер с дискретными величинами. Вот на входе мы имеем, к примеру, дискретный набор значений x_n— замеров величины какого-то сигнала в равные промежутки времени – буфер из N семплов. Тогда с помощью преобразования Фурье можно представить этот сигнал в виде суммы N комплексных чисел X_k:

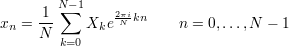
формула 1.

Эти чиcла X_k находятся по явным формулам:

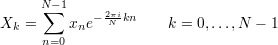
формула 2.

А в чем смысл? Давайте рассматривать индекс n как отсчет времени. Тогда  x_n — это значение сигнала в момент времени n. Рассмотрим величину сигнала в начальный момент времени n = 0:

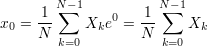
формула 3.

А теперь в момент времени n = 1:

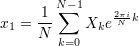
формула 4.

Что изменилось? Если присмотреться, можно заметить, что x₀  представлял собой сумму комплесных чисел X_k.  А x₁— это сумма тех же комплексных чисел X_k, но домноженных на 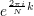, то есть повернутых каждое на свой некоторый угол .

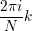Если продолжать отсчитывать время, то заметим, числа "вращаются", причем каждое со своей частотой, зависящей от номера k. И значения  x_n  сигнала в точности равны сумме этих повернутых X_k. Отсюда следует самый главный вывод: каждое из чисел X_k  отвечает какому-то простому колебанию определенной частоты, а сигнал x_n в целом является суммой этих колебаний и это выполняется вкаждый момент времени n от 0 до n – 1.

То есть, мы представили наш сигнал на отрезке времени от 0 до N — 1 как сумму простых колебаний разных частот. В этом и заключается вся суть обработки звука: разложив сигнал в набор колебаний, мы можем оперировать над каждым из этих колебаний (они называются гармониками) в отдельности. А затем по тем же самым формулам можно «собрать» сигнал, который уже можно выводить в звуковое устройство.

Ну и еще немножко об этих числах . Если вспомнить пример с маятником выше, то как раз и получится, что каждое число — это из примера. То есть:

1. аргумент X_k  задает начальную фазу соответствующего колебания;
2. модуль |X_k| — амплитуду гармоники;
3. число отвечает гармонике с частотой 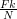, где F — частота дискретизации.

Практически всегда обработка звука затрагивает только амплитуды гармоник, а фазы остаются неизменными. Еще надо заметить, что преобразование Фурье обычно применяется к короткому отрезку сигнала, например 512-4096 семплов. То есть входной сигнал каждые N семплов подвергается преобразованию, обработке, затем обратному преобразованию. И так происходит с каждыми N семплами. Причем на каждом таком отрезке X_k будут, естественно, разными. Кстати, набор чисел X_k называется мгновенным спектром сигнала.

Собственно, делаем

Для преобразования Фурье, а точнее быстрого преобразования Фурье, работающего за N log N, я буду пользоваться библиотекой FFTW. В предыдущей заметке была представлена программа, которая считывает звук порциями с устройства записи и сразу пишет в выход. Теперь расширим ее. Полный пример приложен к статье. В ней добавился код для инициализации библиотеки FFTW и метод process() наконец обрел тело:

void process()

  {

    double inv_n = 1.0 / (double) play_buf_size;

    // конвертируем буфер из ALshort в double, делаем FFT и нормализуем результат

    for (unsigned int i = 0; i < play_buf_size; ++i) dbuf = (double)play_buf / (double)((ALushort)(-1)) * 2.0;
    fftw_execute(p_forward);

    for (unsigned int i = 0; i < play_buf_size; ++i)

    {

      cbuf[0] *= inv_n;

      cbuf[1] *= inv_n;

    }
    // ну, поехали

    transform();
    // делаем обратный FFT и возвращаем обработанный сигнал в буфер

    fftw_execute(p_backward);

    for (unsigned int i = 0; i < play_buf_size; ++i)

    {

      double c = dbuf;

      if ( c > 1.0 ) c = 1.0;

      if ( c < -1.0 ) c = -1.0;
      play_buf = (c * (double)((ALushort)(-1)) ) / 2;

    }

  }

FFTW принимает буфер только из double'ов, поэтому приходится наш буфер play_buf преобразовать в double, причем значения в этом массиве должны быть в пределах от -1.0 до 1.0 (в play_buf они лежат в пределах -32768 — 32768). После выполнения fftw_execute() в массиве cbuf будут лежать комплексные числа  X_k, cbuf[0] — это вещественная часть i-го числа, cbuf[1] — мнимая. Я делю результат преобразования на размер буфера, так как FFTW масштабирует выход в n раз. Поэтому модули всех X_k  будут в пределах 0.0 — 1.0 .

Ну, когда все необходимые приготовления сделаны, вызываем trasform(). Эта функция каким-либо образом меняет амплитуды гармоник (примеры рассмотрим ниже). Затем производится обратное преобразование Фурье, результат которого – это уже измененный сигнал в dbuf. Но его значения имеют тип double и лежат в пределах -1.0 — 1.0, а если не лежат, то по ним надо обрезать. Поэтому надо снова нормализовать их в пределы -32768 – 32767. В таком виде они и отправятся в аудиоустройство.

transform()

Вот здесь и происходит самое интересное. От того, каким образом мы преобразуем спектр cbuf, будет зависеть какой эффект мы получим:

void transform()

  {

    for (unsigned int i = 0; i < play_buf_size; ++i)

    {

      if (i > play_buf_size / 2)

      {

        cbuf[0] = 0.0;

        cbuf[1] = 0.0;

      }

      else

      {

        cbuf[0] = cbuf[0];

        cbuf[1] = cbuf[1];

      }

    }

  }

Мы просто «сжимаем» спектр в два раза, а верхнюю половину его обнуляем. Как видим, обе части комплексного числа надо обрабатывать вместе, чтобы не изменилась фаза гармоники. Если в исходном сигнале присутствовала гармоника с частотой φ, то в преобразованном сигнале она будет соотвествовать гармонике с частотой pi / 2 с той же амплитудой. То есть все частоты в сигнале будут понижены в два раза. Это приводит к снижению тона сигнала на октаву.

Обратного эффекта можно добиться с помощью растяжения спектра в два раза:

  void transform()

  {

    for (unsigned int i = play_buf_size; i > 1; --i)

    {

      cbuf[0] = cbuf[0];

      cbuf[1] = cbuf[1];

    }

  }

В итоге, тон сигнала будет повышен на октаву. А вот старый телефон:

  void transform()

  {

    for (unsigned int i = 0; i < play_buf_size; ++i)

    {

      if ( ((float)i / (float)play_buf_size * 44100.0f) > 3000 )

      {

        cbuf[0] = 0.0;

        cbuf[1] = 0.0;

      }

    }

  }

Суть его проста – обрезаем все частоты выше 3 килогерц. Получаем что-то похожее по звучанию на аналоговую телефонную сеть.

  void transform()

  {

    for (unsigned int i = 0; i < play_buf_size; ++i)

    {

      if ( ((float)i / (float)play_buf_size * 44100.0f) < 3000 )

      {

        cbuf[0] = 0.0;

        cbuf[1] = 0.0;

      }

    }

  }

Вырезает все частоты ниже трех килогерц, что глушит практически весь диапазон звуков, наиболее хорошо слышимых (и воспроизводимых) человеком.

Заключение

Если пропустить музыку через такой фильтр, то хорошо будут слышны разве что тарелки на ударной установке, потому что они издают наиболее широкий шум по всему спектру. Ну вот, собственно и все. Это самое простое, что можно сделать с помощью преобразования Фурье.

Исходники тестового проекта приложены в виде ресурсов непосредственно в архиве с журналом.

Ресурсы

• Ресурс Википедии http://ru.wikipedia.org/wiki/Дискретное_преобразование_Фурье
• Исходники проекта http://mathdev.org/sites/default/files/dsp2.cpp_.zip
• Персональный блог автора http://mathdev.org/mirat