
Последние записи
- Найти среднее значение по данным в ячейке
- Число различных чисел (Microsoft Office Excel)
- Убить процесс
- Конвертер heic в jpg
- Проверка на шестнадцатеричный формат записи
- Отдать пользователю файл с помощью file_get_contents()
- Написать собственую функцию operator[] для битов
- Проблема с движением 2D человека
- OpenGl.Создание винтовой лестницы
- Склеить несколько файлов в один

Интенсив по Python: Работа с API и фреймворками 24-26 ИЮНЯ 2022. Знаете Python, но хотите расширить свои навыки?
Slurm подготовили для вас особенный продукт! Оставить заявку по ссылке - https://slurm.club/3MeqNEk

Online-курс Java с оплатой после трудоустройства. Каждый выпускник получает предложение о работе
И зарплату на 30% выше ожидаемой, подробнее на сайте академии, ссылка - ttps://clck.ru/fCrQw
19th
Авг
 Введение в Scheme. Часть 2.
Введение в Scheme. Часть 2.
Posted by bullvinkle under Журнал, Статьи
Здравствуйте, дорогие читатели. Как и обещал, сегодня мы продолжим рассмотрение наиболее распространенных команд языка Scheme и механизмов, облегчающих управление процессом выполнения, а также познакомимся ближе со средой разработки PLT Scheme.
Продолжение. Начало цикла смотрите в четвертом выпуске журнала…
Введение в Sсheme. Часть 2
Utkin www.programmersforum.ru
Нужно помнить, что данные предикаты нежелательно использовать на неточных числах – ошибки округления могут приводить к обратным результатам. Кстати, определить является ли число точным или не точным можно определить с помощью предикатов:
(exact? z) Тест на точность
(inexact? z) Тест на неточность
Для одного и того же числа один из этих предикатов всегда результат #t, тогда как второй #f. Для сравнения чисел можно использовать следующие предикаты, думаю назначение их понятно и так:
(= х1 х2 х3 …)
(< x1 x2 x3 …)
(> x1 x2 x3 …)
(<= x1 x2 x3 …)
(>= x1 x2 x3 …)
(= 1 1 1) #t
(= 1 2 1) #f
Аналогично, предикатам типов числа, не стоит применять сравнения на неточных числах, поскольку ошибки округления могут дать противоположный результат для почти равных чисел.
Еще предикаты для работы с числами:
(zero? z) Проверка на нуль
(positive? x) Проверка является ли число положительным
(negative? x) Проверка является ли число отрицательным
(odd? n) Проверка является ли число не четным
(even? n) Проверка является ли число четным
Поиск минимального и максимального чисел:
(max x1 x2 …)
(min x1 x2 …)
Примеры:
(max 3 4) Результат 4
(max 3.9 4 9 48 99 5) Результат 99.0 При этом число будет преобразовано в неточное.
(min 54 565 9L0) Результат 9.0
(min 4 4) Результат 4
Нужно соблюдать осторожность при сравнении почти равных неточных чисел, поскольку правильный результат работы данных предикатов не гарантирован. Теперь напомним стандартные арифметические операции:
(+ z1 …) Сложение
(* z1 …) Умножение
(- z1 z2) Вычитание
(- z) Унарный минус
(- z1 z2 …) Вычитание (с произвольным числом аргументов)
(/ z1 z2) Деление (деление на нуль не допускается)
(/ z) Деление 1 / z, при этом образуется дробь
(/ z1 z2 …) Деление z1 на произвольное число аргументов
Теперь примеры (поскольку некоторые результаты не очевидны):
(+ 3 4) Результат 7
(+ 3) Результат 3
(+) Результат 0
(* 4) Результат 4
(*) Результат 1
(- 3 4) Результат -1
(- 3 4 5) Результат -6
(- 3) Результат -3
(/ 3 4 5) Результат 3/20 (3 разделить на 4*5)
(/ 3) Результат 1/3
Кстати, дроби являются точными числами, поэтому их удобно использовать в предикатах для работы с числами (гарантируются однозначные результаты сравнений, отношений и т.д.). Дополнительные операции над числами:
(abs x) Абсолютное значение числа
Дополнительные операции деления:
(quotient n1 n2)
(remainder n1 n2)
(modulo n1 n2)
При этом n2 не должен быть равен нулю (независимо от точности числа). Если n1 / n2 есть целое:
(quotient n1 n2) Результат n1/n2
(remainder n1 n2) Результат 0
(modulo n1 n2) Результат 0
Если в результате n1 / n2 образуется не целое число:
(quotient n1 n2) Результат nq
(remainder n1 n2) Результат nr
(modulo n1 n2) Результат nm
где число nq – n1/n2, округленное к нулю, 0 <| nr | <| n2 |, 0 <| nm | <| n2 |, nr и nm отличаются от n1 множителем n2, nr получит знак n1, nm получит знак n2.
Особенностью этих функций (по сути, вариации на тему нахождение остатка от деления) является факт, того, что они возвращают точные числа, в случае если их входящие параметры также являются точными.
(modulo 13 4) Результат 1
(remainder 13 4) Результат 1
(modulo -13 4) Результат 3
(remainder -13 4) Результат -1
(modulo 13 -4) Результат -3
(remainder 13 -4) Результат 1
(modulo -13 -4) Результат -1
(remainder -13 -4) Результат -1
(remainder -13 -4.0) Результат -1.0 Обратите внимание, результат не точное число.
Следующие функции возвращают наибольший общий делитель или наименьший общий множитель их параметров. Результат является всегда неотрицательным.
(gcd 32 -36) Результат НОД (наибольший общий делитель) 4
(gcd) Результат 0
(lcm 32 -36) Результат НОМ (наименьший общий множитель) 288
(lcm 32.0 -36) Аналогично Результат 288.0, но теперь результат будет неточным.
(lcm) Результат 1
Следующие ниже функции возвращают числитель, и знаменатель дроби (знаменатель всегда положительное число):
(numerator q)
(denominator q)
Примеры:
(numerator (/ 6 4)) Результат 3
(denominator (/ 6 4)) Результат 2
(denominator
(exact->inexact (/ 6 4))) Результат 2.0, для получения неточного числа используется явное преобразование. Естественно удобно и для дробей:
(numerator 6/4) Результат 3 (рассматривается дробь 3/2, и только потом берется знаменатель)
Следующая группа функций:
(floor x)
(ceiling x)
(truncate x)
(round x)
всегда возвращает целые числа. Floor возвращает наибольшее целое число не большее чем х. Ceiling возвращает наименьшее целое число не меньше чем х. Truncate возвращает целое число, которое наиболее ближе к х, и абсолютная величина которого не больше абсолютной величины х. Round возвращает целое число путем округления х (половина икса округляется в большую сторону).
(floor -4.3) Результат -5.0 (числа целые, но не точные)
(ceiling -4.3) Результат -4.0
(truncate -4.3) Результат -4.0
(round -4.3) Результат -4.0
(floor 3.5) Результат 3.0
(ceiling 3.5) Результат 4.0
(truncate 3.5) Результат 3.0
(round 3.5) Результат 4.0 — не точное число
(round 7/2) Результат 4 — точное число
(round 7) Результат 7
(rationalize x y) – возвращает самое простое рациональное число, отличающееся от x не больше, чем y.
Рациональное число x более простое чем другое рациональное число y если x = p1/q1 и y = p2/q2 и и | p1 | < | p2 | и | q1 | <| q2 |. Таким образом, 3/5 более простое число чем 4/7. Хотя не все рациональные числа сопоставимы в этом упорядочении (например, 2/7 и 3/5), любой числовой интервал содержит рациональное число, которое более просто, чем любое рациональное число в том же интервале. Известно также, что 0 = 0/1 – самые простые рациональные числа из всех.
(rationalize
(inexact->exact .3) 1/10) Результат 1/3, точное число
(rationalize .3 1/10) Результат 0.3333333333333333
Трансцендентальные функции:
(exp z)
(log z)
(sin z)
(cos z)
(tan z)
(asin z)
(acos z)
(atan z)
(atan y x)
Здесь все просто, стоит отметить log – имеется ввиду натуральный (а не десятичный), atan с двумя параметрами использует знаки x, y для определения квадранта, к которому принадлежит результат.
(sqrt z) – вычисляет квадратный корень, включая мнимую часть числа:
(sqrt -1) Результат 0+1i (всегда мечтал в Паскале получить корень из -1)
(expt z1 z2) – возведение в степень, довольно-таки мощная функция, единственное ограничение – в степень запрещено возводить нуль.
(expt 2.1 3.3) Результат 11.569741950241465
(expt 2.1 -3.3) Результат 0.08643235124004903
Следующие функции предназначены для поддержки комплексных чисел:
(make-rectangular x1 x2)
(make-polar x3 x4)
(real-part z)
(imag-part z)
(magnitude z)
(angle z)
Здесь x1-x4 вещественные числа, z комплексное.
(make—rectangular x1 x2) Результат комплексное число
(make—polar x3 x4) Результат комплексное число
(real—part z) Результат реальную часть числа (x1)
(imag—part z) Результат мнимую часть числа (x2)
(magnitude z) Результат |x3|
(angle z) Результат xangle
Точные и неточные числа можно преобразовывать следующим образом:
(exact->inexact z)
(inexact->exact z)
Первая функция переводит точное число в неточное, вторая выполняет обратные действия. Естественно, такое преобразование возможно не всегда (такая ситуация считается ошибочной). Теперь рассмотрим ввод и вывод чисел. Числа можно получать из строки следующим образом:
(string->number string)
(string->number string radix)
Здесь radix есть основание системы счисления (точное целое число 2, 8, 10 или 16). Для первого варианта имеется ввиду основание системы счисления равным 10. Если число z является неточным и может быть выраженым с использованием точки в качестве разделителя целой и дробной частями, то число будет представлено с минимально возможным числом разрядов.
(string->number ”100″) Результат 100
(string->number ”100″ 16) Результат 256
(string->number ”1e2″) Результат 100.0
(string->number ”15##”) Результат 1500.0
В случае, если строку в число преобразовать не удастся, результат функции #f.
Пары и списки
Парой (иногда называется точечной парой) называется структура данных, представляющая собой запись, состоящую из двух полей, первое из которых называется car, а вторая cdr (названия сложились исторически). Пара создается функцией сons. Доступ к полям пары осуществляется одноименными функциями car и cdr. Присваивание значений полям пары осуществляется с помощью процедур set-car! и set-cdr!. Основное назначение пар это образование и представление списков. Список может быть определен рекурсивно, как пустой список (список, не содержащий элементов) или как пара поле cdr которого является списком. Если Х является списком, то:
. в Х содержится пустой список
. если список находится в X, то любая пара, поле cdr которой содержит список, находится также в X.
Объекты в полях car последовательных пар списка считаются элементами списка. Например, двухэлементный список это пара, car которой первый элемент списка и чей cdr пара, car которой второй элемент списка и чей cdr есть пустой список. Длина списка – это число элементов (которые можно выразить как число пар).
|
Список |
Список состоит из пар |
||||
|
Пара1 |
Car |
1-й элемент списка |
|||
|
Cdr |
Пара2 |
Car |
2-й элемент списка |
||
|
Cdr |
Пустой список |
||||
Список (a b c d e) можно выразить так (a . (b . (c . (d . (e . ()))))). То есть в списке пары расположены не последовательно друг за другом, а являются вложенными объектами. Пустой список – специальный объект своего собственного типа (это не пара); у него нет никаких элементов, и его длина равна нулю. При этом все списки имеют конечную длину (точное число) и заканчиваются пустым списком.
Для представления пар используется точечная нотация, поля разделяются точкой. Например, пара (4 . 5) имеет поле car 4 и поле cdr 5, при этом внутреннее представление пары будет иным. Списки выражаются проще (х1 х2 … хn), где х это элемент списка. Пустой список выражается, как (). Как уже было отмечено ранее, вся программа на языке Scheme является списком (как и любые ее логически законченные фрагменты), поэтому программы, и выражения можно обрабатывать также как и списки.
Существуют структуры, похожие на списки, которые не удовлетворяют данному выше определению, они называются неподходящие списки. Неподходящий список списком не является, вот его пример:
(a b c . d) что эквивалентно (a . (b . (c . d))), то есть неподходящие списки есть пары.
(define x (list ’a ’b ’c))
(define y x)
y Результат (a b c), list создает список
(list? y) Результат #t, предикат проверки списка
(set—cdr! x 4) Результат не определен (побочный эффект cdr х равен 4)
x Результат (a . 4)
(eqv? x y) Результат #t
y Результат (a . 4)
(list? y) Результат #f
(set—cdr! x x) Результат не определен
(list? x) Результат #f
Предикат (pair? obj) проверяет является ли объект парой.
(pair? ‘(a . b)) Результат #t
(pair? ‘(a b c)) Результат #t
(pair? ‘()) Результат #f
(pair? ’#(a b)) Результат #f
Следующая функция возвращает пару:
(cons obj1 obj2)
car пары будет представлять собой obj1, cdr соответственно obj2.
(cons ‘a ‘()) Результат (а)
(cons ‘(a) ‘(b c d)) Результат (c d)
(cons “a“ ‘(b c)) Результат (”a“ b c), обратите внимание на квотирование и кавычки
(cons ’a 3) Результат (a . 3)
(cons ’(a b) ’c) Результат ((a b) . c)
Квотирование в данном случае используется для того, чтобы поля пары не вычислялись в момент внесения в пару. Это позволяет вносить в пару как простые данные, вроде чисел, так и функции и выражения.
(car pair) – возвращает поле car пары (так и хочется сказать первое поле, но внутреннее представление пар может быть иным, поля пары могут находиться даже не в смежных областях памяти). Попытка получения car пустой пары вызовет ошибку.
(car ’(a b c)) Результат a
(car ’((a) b c d)) Результат (a)
(car ’(1 . 2)) Результат 1
(car ‘()) Результат ошибка вычислений
(cdr pair) – возвращает поле cdr пары. Получение cdr пустого списка вызовет ошибку.
(cdr ‘((a) b c d)) Результат (b c d)
(cdr ’(1 . 2)) Результат 2
(cdr ’()) Результат ошибка вычислений
(set—car! pair obj) и (set—cdr! pair obj) помещает соответственно в car и cdr пары pairs объект obj.
Результат их работы не определен, функции имеют побочные эффекты. Очень часто во время манипуляций со списками возникает много car и cdr. Такие выражения допускается сокращать:
(car (cdr (cdr x))) эквивалентно caddr, то есть справедливо следующее утверждение:
(define caddr (lambda (x) (car (cdr (cdr x)))))
Правило формирования функции следующее: все car представляются как а, а все cdr как d в наименовании функции, которая начинается с с и заканчивается r. При этом допускается формирование функций не более чем из четырех car и cdr.
(null? obj) – возвращает #t, если obj есть пустой список
(list? obj) – возвращает #t, если obj есть список.
(list? ‘(a b c)) Результат #t
(list? ’()) Результат #t
(list? ‘(a . b)) Результат #f
(let ((x (list ’a)))
(set-cdr! x x)
(list? x)) Результат #f
(list obj …) – создает список.
(list ’a (+ 3 4) ’c) Результат (a 7 c)
(list) Результат ()
(length list) – передает число элементов в списке
(length ’(a b c)) Результат 3
(length ’(a (b) (c d e))) Результат 3
(length ’()) Результат 0
(append list …) – объединение списков, при этом происходит перераспределение их внутренней структуры (таким образом, чтобы результат удовлетворял определению списка).
(append ‘(x) ‘(y)) Результат (x y)
(append ’(a) ’(b c d)) Результат (a b c d)
(append ’(a (b)) ’((c))) Результат (a (b) (c))
(append ’(a b) ’(c . d)) Результат (a b c . d)
(append ‘() ‘a) Результат a, список был изменен.
(reverse list) – возвращает список, перераспределенный в обратном порядке.
(reverse ’(a b c)) Результат (c b a)
(reverse ’(a (b c) d (e (f)))) Результат ((e (f)) d (b c) a)
(list-tail list k) – возвращает список на основе списка list, но без k первых элементов. Входящий список должен содержать не менее k элементов. Работу list-tail можно выразить функцией-эквивалентом:
(define list-tail
(lambda (x k)
(if (zero? k)
x
(list-tail (cdr x) (- k 1)))))
(list-ref list k) – возвращает k-й элемент списка. В списке должно быть не менее k элементов.
Нумерация элементов списка осуществляется от нуля. Плюсом пар и неподходящих списков является возможность создания древовидных структур данных с неограниченным числом узлов (пока хватит памяти компьютера).
Символы
Это специальные объекты, особенность которых заключается в том, что символы считаются эквивалентными (для предиката eqv?), если получены одинаковым путем. Символы в частности могут представлять идентификаторы программы, и их уникальность дает возможность использовать их во внутреннем представлении программы. Правила образования символов полностью соответствуют правилам образования идентификаторов. Не следует путать данные символы (Symbols) с символами строки (Characters). Это символы программы и не предназначены для представления строк (хотя и могут быть конвертированы в строки). В частности символы можно получить, квотировав идентификаторы.
Следующий предикат подтверждает, все то, что сказано выше:
(symbol? obj) – определяет является ли объект символом.
(symbol? ’foo) Результат #t
(symbol? (car ’(a b))) Результат #t
(symbol? “bar“) Результат #f, строки представляются строковыми символами!
(symbol? ‘nil) Результат #t
(symbol? ‘()) Результат #f
(symbol? #f) Результат #f
(symbol? 5) Результат #f
(symbol? ‘5) Результат #f, это не идентификатор и не выражение
Для преобразования символов в строки используется
(symbol->string symbol)
Примеры:
(symbol->string ’flying-fish) Результат “flying-fish”
(symbol->string ’Martin) Результат “martin”
(symbol->string
(string->symbol ”Malvina”)) Результат “Malvina”
Здесь (string->symbol “Malvina“) выполняет обратную функцию.
(string->symbol “Привет“)
Символы, в частности, предоставляют программисту возможность работать с объектами программы через операции над их идентификаторами.
Строковые символы
Строковой символ – минимальная единица представления текстовой информации. Строковые символы можно образовывать так #\<character> или #\<character name>. Вот примеры образования строковых символов:
#\a; буква в нижнем регистре
#\A; буква в верхнем регистре
#\(; открывающая скобка
#\ ; пробел
#\space; пробел (образование строкового символа по его имени)
#\newline; символ перехода на новую строку
Поскольку Scheme во многом система, не зависящая от конкретной платформы, то получать константы строковых символов по кодам в какой-либо кодировке не допускается. Поэтому нельзя получить строковой символ #\13, в тоже время PLT Scheme позволяет получать символы национальных алфавитов и задать строковый символ #\й вполне допустимо. Для определения факта того, что объект является строковым символом, используется следующая функция:
(char? obj) – возвращает #t, если объект является строковым символом.
(char? ‘try) Результат #f, поскольку язык проводит четкую границу между символами и строковыми символами.
Все строковые символы определяются на основе их порядка следования в алфавите. Поэтому между строковыми символами существуют отношения, связанными с их расположением относительно друг друга. Для оценки строковых символов используется ряд функций:
(char=? char1 char2)
(char<? char1 char2)
(char>? char1 char2)
(char<=? char1 char2)
(char>=? char1 char2)
Сначала следуют цифры, потом прописные буквы, потом строчные (национальные символы «больше» латиницы). Кстати, PLT Scheme версии 350 допускает более двух символов для сравнения (на манер числовых предикатов).
(char-ci=? char1 char2)
(char-ci<? char1 char2)
(char-ci>? char1 char2)
(char-ci<=? char1 char2)
(char-ci>=? char1 char2)
Тоже самое, но без учета регистра.
(char-ci=? #\A #\a)
Результат #t. Аналогично, функции с приставкой –ci в PLT Scheme могут содержать больше чем два аргумента.
(char-alphabetic? char) – возвращает #t, если строковой символ буква.
(char-numeric? char) – возвращает #t, если строковой символ цифра.
(char-whitespace? char) – возвращает #t, если строковой символ пробел.
(char-upper-case? letter) – возвращает #t, если строковой символ буква в верхнем регистре.
(char-lower-case? letter) – возвращает #t, если строковой символ буква в нижнем регистре.
Несмотря на то, что задавать константы строковых символов их кодами нельзя, получать коды из строковых символов разрешено: (char->integer char) – вернет точное целое число, которому сопоставлен данный строковой символ. Обратная ей функция (integer->char n). Изменить регистр символов можно с помощью функций:
(char—upcase char) – изменяет регистр строкового символа на верхний
(char—downcase char) – изменяет регистр строкового символа на нижний.
Строки
Строки это последовательности символов. В Scheme строки выделяются кавычками. В строки допускается включать Escape-последовательности через использование обратного слеша (\). Например, если известны коды символов, то строку можно задать следующим образом: “\u65\u65” (чего нельзя делать для строковых символов). Длина строки есть число содержащихся в ней символов (точное целое неотрицательное число). Индексация символов начинается от нуля. Аналогично операций с символами все функции имеющие приставку –ci есть операции со строками без учета регистра. Начнем с определения строки:
(string? obj) – возвращает #t, в случае, если объект является строкой.
Существует два способа напрямую создать строку с помощью функций:
(make-string k)
(make-string k char)
Здесь, k – есть длина создаваемой строки, char – символ, которым должна быть наполнена строка (в первой функции она будет наполнена символами вида ”\u0000\u0000\u0000”). Также строки можно создавать путем конкатенации (объединении) символов:
(string char …)
Длина строки:
(string-length string)
Можно также получить доступ к каждому элементу строки (строковому символу):
(string-ref string k)
(string-ref “Привет” 1) Результат #\р, так как нумерация в строке идет от нуля
Изменить конкретный символ в строке можно с помощью: (string—set! string k char). При этом следует помнить, что string—set! возвращает неопределенное значение. Строки можно сравнивать (на порядок расположения в них строковых символов):
(string=? string1 string2)
(string-ci=? string1 string2)
(string<? string1 string2)
(string>? string1 string2)
(string<=? string1 string2)
(string>=? string1 string2)
(string-ci<? string1 string2)
(string-ci>? string1 string2)
(string-ci<=? string1 string2)
(string-ci>=? string1 string2)
PLT Scheme разрешает использовать более двух аргументов при сравнении строк.
(string=? “12″ “15″ “gsjfds”) Результат #f
При этом более короткие строки считаются меньше длинных:
(string-ci<? “fff” “ffff”) Результат #t
Выделение подстроки:
(substring string start end)
При этом входящие параметры должны удовлетворять условию:
0 < start < end < (string-length string)
Объединение (конкатенация) строк:
(string—append string …)
(string—append “Привет ” “Мир!”) Результат “Привет Мир!”
Также важны функции преобразования строк:
(string->list string) – преобразование строки в список строковых символов
(list->string list) – преобразование списка в строку (список должен быть списком строковых символов)
(string->list string) и (list->string list) являются противоположными по отношению друг к другу.
(string-copy string) – возвращает копию строки
Векторы
Векторы в Scheme есть неоднородные структуры данных индексированные целыми числами. Одним из плюсов векторов является организация, построенная таким образом, что скорость доступа к ним выше, чем к спискам. Длина вектора есть число элементов, которые он содержит (целое точное неотрицательное число, также как и индекс любого из доступных элементов вектора). Индексация элементов вектора начинается от нуля. В общем, векторы сильно похожи на массивы императивных языков программирования, но имеют одну приятную особенность – вектор может содержать данные различных типов.
Для записи векторов используется следующая нотация: #(obj …).
#(0 (2 2 2 2) ”Anna”) Вектор, состоящий из трех элементов – числа нуль, списка (2 2 2 2) и строковой константы ”Anna”.
(vector? obj) – определяет, является ли объект вектором (#t если объект вектор).
(make—vector k) – создает вектор из k элементов, сами элементы не определены.
(make—vector k fill) – создает вектор из k элементов, элементы которого являются fill.
(vector obj …) – создает вектор из указанных объектов.
(vector ‘a ‘b ‘c) Результат #(a b c), сами элементы при этом не вычисляются (из-за одинарной кавычки).
(vector-length vector) – возвращает длину вектора (точное целое число).
(vector-ref vector k) – возвращает k-тый элемент вектора (k как и все индексы должен быть точным и целым).
(vector-ref ’#(1 1 2 3 5 8 13 21) 5) Результат 8 (нумерация от нуля).
(vector—set! vector k obj) – присваивает k-тому элементу вектора значение obj. Результат не определен, функция обладает побочными эффектами.
(vector->list vector) – создает список из вектора.
(list->vector list) – создает вектор из списка.
(vector->list ’#(dah dah didah)) Результат (dah dah didah)
(list->vector ’(dididit dah)) Результат #(dididit dah)
(vector-fill! vector fill) – заполняет указанный вектор объектами fill. Результат функции не определен, функция имеет побочные эффекты.
Особенности управления
Здесь мы опишем некоторые (не все, например, отложенные вычисления уже рассматривались) механизмы, облегчающие управление процессом выполнения.
(procedure? obj) – возвращает #t, в случае если перед нами процедура. Надо отметить, что в Scheme очень часто идет слияние понятий функция и процедура.
(procedure? car) Результат #t
(procedure? ’car) Результат #f
(procedure? (lambda (x) (* x x))) Результат #t
(procedure? ‘(lambda (x) (* x x))) Результат #f
(apply proc arg1 … args) – вызывает указанную функцию к аргументам заданным списком.
(apply + (list 3 4)) Результат 7, для функции + (плюс) задается параметр (только один), заданный в виде списка.
(map proc list1 list2 …) – применение функции proc к каждому из списков. Списки должны иметь одинаковый размер. Одна из мощнейших функций языка. Работает это следующим образом:
(map car ‘((a b) (d e) (g h))) Результат (a d g)
(map cdr ‘((a b) (d e) (g h))) Результат ((b) (e) (h))
(map cadr ‘((a b) (d e) (g h))) Результат (b e h)
Функция всегда работает со списками и списки же и возвращает. Эти примеры не полностью раскрывают работу функции, вот еще примеры:
(map + ’(1 2 3) ’(4 5 6)) Результат (5 7 9)
(map + ‘(1 2 3) ‘(4 5 6) ‘(7 8 9)) Результат (12 15 18)
(define my-list ‘(1 2 3 4 5))
(define (square val) (* val val))
(map square my-list) Результат (1 4 9 16 25)
(for—each proc list1 list2 …) —
аналогична map, но используется в основном для функций с побочными эффектами, результат которых не определен.
(let ((v (make-vector 5)))
(for-each (lambda (i)
(vector-set! v i (* i i)))
‘(0 1 2 3 4))
v)
Результат #(0 1 4 9 16). Создаем вектор v из пяти элементов. Затем применяем (lambda (i) к вектору v. Заносим данные из списка ‘(0 1 2 3 4) (который сразу не вычисляется из-за одинарной кавычки) следующим образом: в вектор v записывается элемент списка, умноженный сам на себя (запись осуществляется посредством vector—set!, при этом в качестве индексов для доступа к вектору используется все тот же список ‘(0 1 2 3 4)). После выхода из блока let вектор v будет разрушен, а его содержимое будет передан как результат работы блока let.
PLT Scheme
Теперь немного подробней о самой IDE. PLT Scheme состоит из нескольких компонентов:
. MrEd – расширение MzScheme для графического программирования
. DrScheme – среда проектирования
. Mzc – компилятор в байт-код, не зависимый от платформы (позволяет создавать переносимые приложения)
. MzScheme3m – экспериментальная версия MzScheme, особенность которой более точное управление распределением памятью (в сравнении MzScheme).
MzScheme, основной компилятор, интерпретатор, и система поддержки исполнения программ. Кроме того, PLT Scheme, содержит в себе не только описанный выше стандарт R5RS, но также дополнительные возможности, а именно:
. система поддержки пространства имен и управления трансляцией
. поддержка механизма исключений
. приоритетные потоки
. классы и система объектов
. регулярные выражения
. расширенная поддержка макросов
. поддержка хэшей (как встроенного типа данных)
. поддержка юникода.
И более того, PLT Scheme содержит также группу диалектов Scheme, каждый из которых имеет свои задачи (например, есть диалект специально адаптированный для изучения функционального программирования студентами высших учебных заведений). Так как система построена в минималистичном и строгом стиле рекомендуется начинать изучение с DrScheme (он не так суров, и не сильно отпугивает пользователей привыкших к обилию кнопок, картинок и иконостасу на Рабочем столе). Его-то мы и рассмотрим подробней.
Как уже упоминалось ранее, DrScheme имеет два окна, одно предназначено для ввода текста программы, второй есть командный интерпретатор (команды, введенные в него, исполняются немедленно, что удобно для изучения языка). В последнее же окно выводится и сообщения от drScheme, именуемое как главная текстовая область (см. рисунок 1):
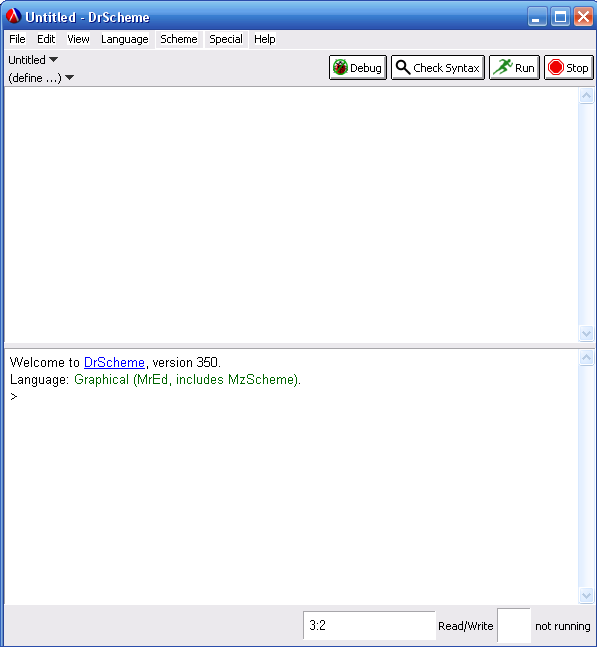
Рис. 1. Среда drSheme
Поскольку PLT Scheme поддерживает несколько языков программирования, то прежде чем приступить к работе, нужно выбрать* соответствующий язык программирования Language|Choose Language (см. рисунок 2):
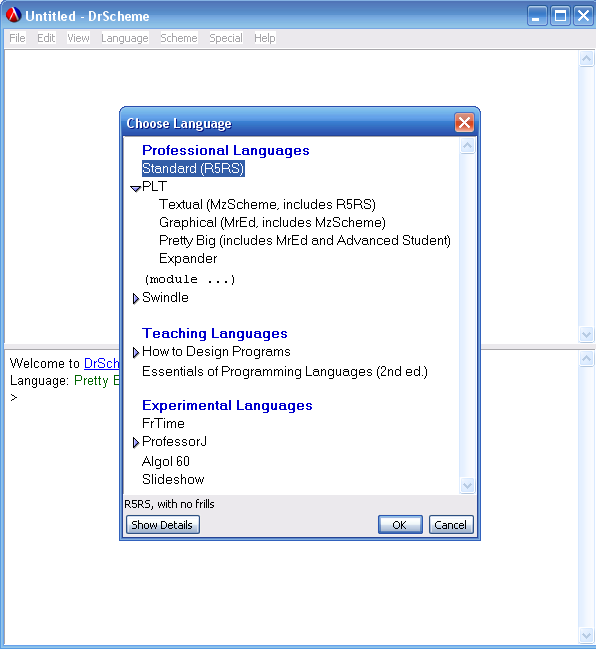
Рис. 2. Выбор языка
* Комментарий автора
наименование пунктов меню может немного отличаться в зависимости от версии среды разработки
Стандарт языка называется Standart (R5RS), для освоения материала статьи его вполне достаточно. Остальные диалекты отличаются различными свойствами, в том числе и поддержкой графического интерфейса пользователя. PLT Scheme запоминает последний выбранный диалект и при следующем запуске сразу же готов работать в выбранном контексте.
Изюминкой PLT Scheme является возможность компиляции текстов программ. Исторически и по ряду объективных причин большинство реализаций Scheme есть интерпретаторы. Однако готовые к употреблению программы без стороннего окружения также необходимы (что, кстати, требуют и решаемые задачи, круг которых гораздо шире в PLT Scheme, чем в голом стандарте R5RS). Чтобы получить из текста программы на языке Scheme вполне функциональный exe-файл требуется, чтобы программа была введена в окно ввода программы (обычно оно первое) (см. рисунок 3). А также чтобы она была уже сохранена во внешнем файле.
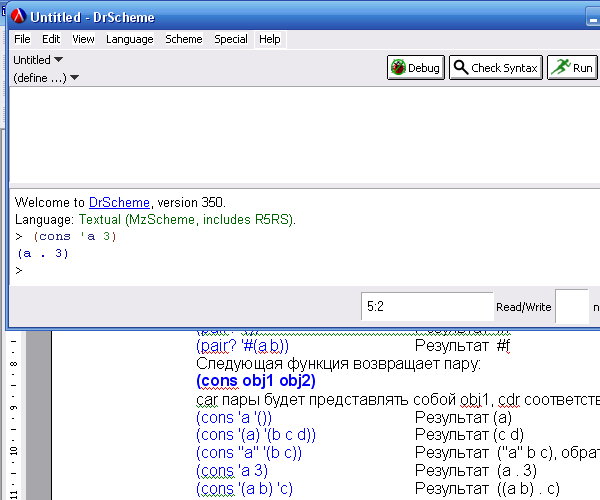
Рис. 3. Работа с примером
Затем выбираем пункт меню Scheme|Create Executable… Далее необходимо выбрать тип исполнения файла (см. рисунок 4):
. Launcher
. Stand-alone
. Distribution.
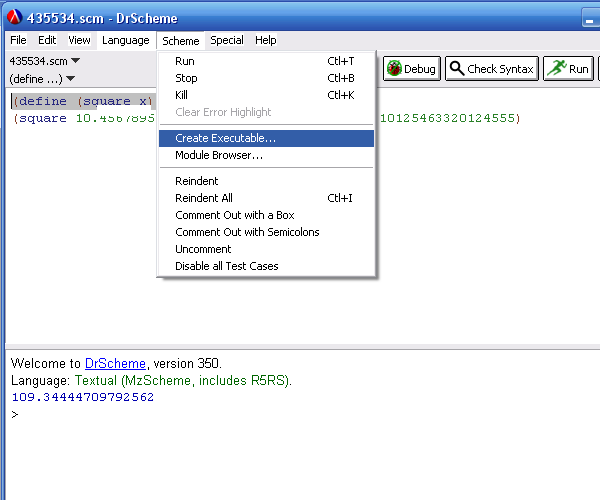
Рис. 4. Создание исполняемого файла
Для простых учебных примеров Stand—alone вполне достаточно (однако, если необходимо использовать программу на другом компьютере, то потребуется перетащить некоторые библиотеки).
Заключение
Введение дает только элементарные азы и рассчитано на плавный переход от императивного стиля к функциональному. Данное введение не дает представления о функциональном программировании – это просто справочник наиболее распространенных команд языка Scheme, также знакомство с конкретной средой разработки PLT Scheme. Более полное и подробное руководство по PLT Scheme можно найти на сайте проекта (на английском языке), статья предназначена быть отправной точкой для дальнейшего самостоятельного обучения. Дополнительно можно отметить возможность встраивания Scheme и в другие языки программирования (как встроить Scheme в Дельфи, можно узнать здесь: http://www.orlovsergei.com/Progs/Scheme/SchemeToDelphi.htm). Плюсы такого союза очевидны, например, это удобно для работы с длинной арифметикой.
Ресурсы
. Лисп как альтернатива Java http://alexey.tamb.ru/scheme/lisp-scheme-java.html
. Сайт «схемщиков» http://schemers.org
. PLT Scheme http://www.plt-scheme.org
. Дополнительные библиотеки для PLT Scheme http://planet.plt-scheme.org
. Неформальное введение в Scheme http://ru.wikibooks.org/wiki/Введение_в_язык_Scheme_для_школьников
Обсудить на форуме — Введение в Scheme. Часть 2.
Похожие статьи
Купить рекламу на сайте за 1000 руб
пишите сюда - alarforum@yandex.ru
Да и по любым другим вопросам пишите на почту

пеллетные котлы

Пеллетный котел Emtas

Наши форумы по программированию:
- Форум Web программирование (веб)
- Delphi форумы
- Форумы C (Си)
- Форум .NET Frameworks (точка нет фреймворки)
- Форум Java (джава)
- Форум низкоуровневое программирование
- Форум VBA (вба)
- Форум OpenGL
- Форум DirectX
- Форум CAD проектирование
- Форум по операционным системам
- Форум Software (Софт)
- Форум Hardware (Компьютерное железо)


