
Последние записи
- Windows 10 сменить администратора
- Рандомное слайдшоу
- Событие для произвольной области внутри TImage
- Удаление папки с файлами
- Распечатка файла
- Преобразовать массив байт в вещественное число (single)
- TChromium (CEF3), сохранение изображений
- Как в Delphi XE обнулить таймер?
- Изменить цвет шрифта TextBox на форме
- Ресайз PNG без потери прозрачности

Интенсив по Python: Работа с API и фреймворками 24-26 ИЮНЯ 2022. Знаете Python, но хотите расширить свои навыки?
Slurm подготовили для вас особенный продукт! Оставить заявку по ссылке - https://slurm.club/3MeqNEk

Online-курс Java с оплатой после трудоустройства. Каждый выпускник получает предложение о работе
И зарплату на 30% выше ожидаемой, подробнее на сайте академии, ссылка - ttps://clck.ru/fCrQw
24th
Май
 Определитель матрицы
Определитель матрицы
Изучаю тут незнакомый мне доселе метод треугольников..
Интересуют матрицы от 4 порядка и выше..
В книге написано, что для 4 порядка вычисление определителя сводится к 24 слагаемым у меня получилось всего 8… но ответ по определителю верный..может я что не так поняла..
Вот вырезки из книги.. (читать всё…)
16th
Май
 Идея алгоритма сжатия методом деления.
Идея алгоритма сжатия методом деления.
Привет, приснилась сегодня простая мысль: допустим файл — последовательность чисел, ну скажем 2345678543….xxxx и тд. Если впереди последовательности поставить точку, то получим 0.2345678543. Теперь уравнение: x / y = 0.2345678543….xxxx. Осталось найти X и Y и их сохранить в новый файл. Затем просто поделив x на y мы получим исходную последовательность.
Бред, да? (читать всё…)
9th
Дек
 Реакция программы на звук в микрофон
Реакция программы на звук в микрофон
Подскажите как научить программу реагировать на звук из микрофона. К примеру что бы при хлопке происходило какое нибудь действие в программе.
21st
Окт
 Как можно реализовать алгоритм сортировки массива по возрастанию методом сортировки выбором?
Как можно реализовать алгоритм сортировки массива по возрастанию методом сортировки выбором?
Вот что-то вроде такого:
30th
Сен
 x64 ассемблер и алгоритмы
x64 ассемблер и алгоритмы
Вот решил наконец попробовать x64 попрограмить. Вроде все круто – 64-битные регистры + 8 дополнительных регистров. Итого теперь наконец стало в общей суме 16 базовых регистров. Ну что я рассказываю, каждый наверняка введение краткое читал.
У меня другой вопрос: вот кто-то ощутил уже на себе преимущества 64-битных регистров против 32-битных? Ну там не знаю, мож у вас MD5 началось в 2 раза быстрее считаться, или там crc32 в четыре раза? Или не знаю… Как кто юзает ассемблер для x64? Есть ли какие-то реальные примеры известных алгоритмов, заоптимизированных для x64 на ассемблере? Покажите пожалуйста..
PS: Что-то погуглил на тему примеров сорцов в гугле – непонятная тишина… Все на шарпах и явах чтоле пишут? )
конкретно алгоритмов заоптимизированных для x64 нет. В основном алгоритмы пишут на С/С++ а они уже в свою очередь компилируются под нужную платформу.
главное преимущество x64 систем – фактически нет ограничения на размер используемой виртуальной памяти. В 32-битных версиях Windows максимальный размер виртуальной памяти для одного приложения 2 ГБ, в 64-битных версиях 8 ТБ. 2 ГБ памяти слишком мало для серверных приложений.
Для обычных пользователей 64-битные системы почти не дают преимуществ, а для серверов 64-битные системы довольно-таки нужная весчь.
есть ещё куча преимуществ и недостатков но приводить их всех лень
19th
Июн
 Правильное определение порядка точек в прорисовке тени в 2d-игре
Правильное определение порядка точек в прорисовке тени в 2d-игре
Давно тут не постил уже, прям забыл уже как тут хорошо было

Вот заинтересовал вопрос о прорисовке тени. Допустим есть некий игрок и препятствия (см. вложение) и он имеет угол обзора 90 градусов и все, что выпадает за этот угол или закрывается препятствием не должно быть отображено. Допустим неким образом я сумел просчитать координаты этих точек, где кривая тени ломается. Определяю методом перебора:
1. Проверяю доступность для “обзора” каждой из четырех точек препятствия (все объекты – прямоугольники).
2. Если точка оказывается доступной(красные круги) то добавляем ее в список точек а также пробуем спроектировать луч из этой точки с углом из точки обзора, тем самим добавляя спроектированную точку в список(угол показан жёлтым, а спроектированная точка зелёным).
3. Дальше пытаюсь отсортировать эти точки так, чтобы их можно было бы прорисовать одним циклом (для начала просто соединить в ломанную(показано белым), а в дальнейшем хочу зарисовать все, не входящее в эту фигуру чёрным или серым). Но так как все препятствия расположены хаотически то может случится ситуация, когда одно препятствие попадает в список раньше положенного.
Прошу помощи в сортировке такого списке, чтобы можно было отобразить как на картинке  Спасибо за внимание.
Спасибо за внимание.
Интересная проблема и возможные варианты решения. Смотрим на форуме. Принимаем участие.
31st
Май
 Алгоритм Брезенхема
Алгоритм Брезенхема
Рисование прямой методом Брезенхема.
procedure TForm1.Button1Click(Sender: TObject);
var
x1,x2,y1,y2,dx,dy,s1,s2,x,y,o,i,v,obmen : integer;
begin
x1:=strtoint(edit1.Text);
y1:=strtoint(edit2.Text);
x2:=strtoint(edit3.Text);
y2:=strtoint(edit4.Text);
x:=x1;
y:=y1;
dx:=(abs(x2-x1));
dy:=(abs(y2-y1));
if (x2-x1)<=0 then s1:=-1 else s1:=1;
if (y2-y1)<=0 then s2:=-1 else s2:=1;
if dy>dx then
begin
v:=dx;
dx:=dy;
dy:=v;
obmen:=1;
end
else obmen:=0;
o:=2*dy-dx;
for i := 1 to dx do
begin
form1.Canvas.Pixels[x,y]:=clBlack;
while o>=0 do
begin
if obmen=1 then
x:=x+s1
else
y:=y+s2;
o:=o-2*dx;
end;
if obmen=1 then y:=y+s2
else x:=x+x1;
o:=o+2*dy;
end;
//form1.refresh;
//self.Repaint;
end;
25th
Май
 Поиск пути
Поиск пути
Многие начинающие игроделы сталкиваются с проблемой автоматической прокладки маршрутов ботами на карте. Основных проблем две – генерация вейпоинтов и прокладка по ним кратчайшего (либо оптимального по другим параметрам) маршрута. Данная статья, делает небольшой экскурс по реализации алгоритма поиска кратчайшего пути по ранее установленным вейпоинтам (на основе алгоритма Дейкстры).
ПОИСК ПУТИ
На пути постижения мудрости не надо бояться, что свернёшь не туда.
Пауло Коэльо
Автор Utkin www.programmersforum.ru
Прокладка маршрута называется навигацией. Она бывает двух видов: автономная – когда объект (бот) самостоятельно прокладывает маршрут из одной точки карты в другую, запоминает его индивидуально (либо в общем, хранилище маршрутов для одной группы юнитов), и предварительная – когда маршруты уже проложены во время проектирования карты (опять же автоматически или программистом), или же на этапе загрузки карты игрового мира. Маршрут обычно представляет собой некоторую совокупность точек (или их координат) со связями между ними, то есть это маршрут, проложенный на графе. Сами точки называются вейпоинтами – это углы (или вершины) графа. Соответственно подавляющее большинство алгоритмов поиска пути есть алгоритмы по работе с графами.
Краткий экскурс…
Наиболее простой способ – это проложить ключевые точки уже на карте (в момент ее проектирования), а уже на основании имеющейся информации вырабатывать маршрут в зависимости от игрового процесса. Как уже было указано выше, маршрут имеет не только точки, но также и взаимосвязи между ними. В самом простом случае это ссылки на те точки, на которые можно попасть из данной точки, а также отношения между ними (например, это может быть время прохождения или расстояние между точками). В случае если вейпоинты генерируются до игры (во время разработки карты, а не ботом во время игрового процесса) отношения также должны быть уже рассчитаны (например, как расстояния между доступными точками). Также иногда некоторые маршруты уже изначально заложены и бот «знает» куда идти, но такой вариант должен комбинироваться с алгоритмами самостоятельной выработки маршрута по ряду причин – это делает игровой процесс более динамичным, карта может изменять свои параметры (например, произошел обрыв моста, тогда связи, отношения между двумя точками разрушаются, и требуется новый путь) и т.д.
Особенностью игрового мира является тот факт, что любая ситуация может быть промоделирована, поэтому для простых карт (имеющих малое количество вейпоинтов) можно просчитать оптимальные маршруты до каждой точки на этапе проектирования карты. Для карт, имеющих большое количество вейпоинтов, можно просчитать оптимальные маршруты только для тактически важных точек (какие это точки определяет разработчик), например, от базы до основных ресурсов или от одной лестницы до другой и т.д., остальные маршруты все равно придется просчитывать во время игры.
Предварительный просчет точек осуществлен, например, в игре StarСraft. Это видно если отправить рабочего добывать ресурсы, он смело перемещается через туман войны и по неисследованной области, способен находить подъемы на другой уровень плоскости и сразу определять местоположение моста.
Алгоритм Дейкстры
Этот алгоритм находит кратчайшее расстояние от одной из вершин графа до всех остальных.
Сначала рассмотрим граф без применения алгоритма Дейкстры, это упростит понимание алгоритма в дальнейшем. Для удобства восприятия обозначим каждую вершину идентификатором, пусть это будет номер вершины (порядок нумерации на графе значения не имеет). В качестве отношения между точками возьмем расстояние. Получается, точка имеет: идентификатор, список точек, куда можно попасть из данной точки и расстояния до каждой из доступных точек.
Вот образец графа (см. рисунок 1):
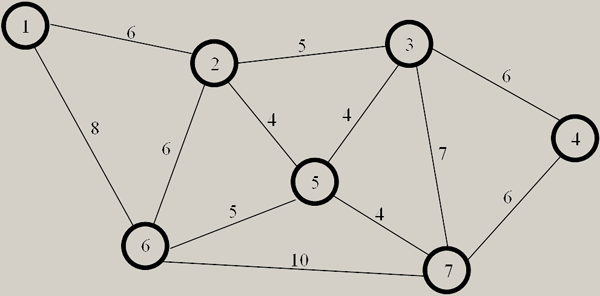
Рис. 1. Образец типичного графа
Представьте, что нам нужно попасть из точки 1 в точку 5. Сколько имеется путей достижения точки 5? Давайте посчитаем:
а) 1-2-5
б) 1-2-6-5
в) 1-6-5
г) 1-6-2-5
Итого четыре маршрута. Вычислим расстояния по каждому маршруту (суммированием расстояний между точками). Вот расстояния между точками:
а) 1-2 расстояние 6
б) 2-5 расстояние 4
в) 2-6 расстояние 6
г) 6-5 расстояние 5
д) 1-6 расстояние 8
е) 6-2, он же 2-6 расстояние 6
Общее расстояние всего маршрута:
а) 1-2-5 расстояние 6+4=10
б) 1-2-6-5 расстояние 6+6+5=17
в) 1-6-5 расстояние 8+5=13
г) 1-6-2-5 расстояние 8+6+4=18
Самый оптимальный (для нашего примера) является путь а) расстояние всего 10. Если же будут обнаружено два и более маршрутов, имеющих одинаковую длину, то выбирается, как правило, первый (либо заранее продумано, какой из маршрутов, лишь бы выбор был осуществлен).
Также нужно обратить внимание, что на первый взгляд маршруты б) и г) равны (казалось бы, от перемены мест слагаемых сумма не меняется), однако следует не забывать, что идентификаторы здесь не несут математического смысла это просто имена точек. Таким же образом мы могли бы назвать и a, b, c и т.д. Операции идут над расстояниями, а суммы пар расстояний (1-2; 2-6) и (1-6; 2-6) не эквивалентны (не равны) между собой.
Теперь сам алгоритм. Он предназначен для поиска всех наикратчайших путей от указанной вершины до всех остальных. Изначально расстояния нам не известны, поэтому будем считать, что они равны максимально возможному расстоянию до каждой из вершин (точек) графа (кроме исходной, до нее расстояние естественно равно нулю). Далее, необходимо отмечать рассмотренные точки графа (чтобы не повторяться)…
Перейдем к алгоритму
Итак, рассмотрим действие алгоритма для первой вершины нашего графа. Вершина 1 имеет отношения (в дальнейшем будем считать отношения просто расстояниями между вершинами графа) с вершинами 2 и 6. Ближайшей точкой будет являться точка 2, поскольку расстояние до нее меньше и составляет 6 единиц (в примере неважно каких единиц, в игре это могут быть условные единицы реальных км, м и т.д., единицы местоположения юнита на карте, число пикселей с привязкой к координатной сетке области отображения и т.д.). Считаем точку 1 пройденной, поскольку нам известны кратчайшие расстояния до точек 2 и 6.
Следующей рассмотрим точку 2 (потому что она ближе к 1 точке). Для нашего графа соседями точки 2 являются 1, 6, 5 и 3. Точку 1 мы рассматривать не будем, поскольку уже было отмечено, что она была просмотрена ранее. Вот расстояния:
. до точки 6 расстояние 6;
. до точки 5 расстояние 4;
. до точки 3 расстояние 5.
Отсюда следует, что ближайшей точкой к вершине 2 будет точка 5, поскольку расстояние до нее минимально, по сравнению с вершинами 6 и 3.
На данном этапе:
. расстояние до точки 1 составляет 0;
. расстояние до точки 2 составляет 6;
. расстояние до точки 5 составляет 10 (6+4);
. маршрут до точки 5 следующий – 1-2-5 (и никакой другой до данной точки более не рассматривается);
. следующей точкой будет являться точка 5;
. точка 2, также как и точка 1 считается отмеченной и больше не рассматривается;
. расстояние до точки 6 (маршрут 1-6) равен 8 (0+8), а не 12 (маршрут 1-2-6, расстояние 6+6), поскольку хоть точка 6 и не отмечена, но текущее расстояние до нее уже было вычислено и оно менее текущего (не забываем, что изначально расстояние до каждой точки равно максимально возможному для данного графа).
Собственно этих данных достаточно для того, чтобы выполнить следующие итерации для всех оставшихся точек нашего графа. Несмотря на такое простое описание реализации алгоритма Дейкстры может оставаться трудной, если не представлять, в виде каких структур выражать работу алгоритма. Вот классический вариант:
Представление точек графа
Граф можно представлять многими способами, например, в виде таблицы смежности (ru.wikipedia.org/wiki/Список_ребер). Такой способ представления удобен с математической точки зрения, но абсолютно не удобен с практической. Например, точку можно представить как ее координаты и набор отношений (где отношение можно представить как пару – указатель на точку-соседа и расстояние до точки-соседа). Если отношение представляет собой расстояние между двумя точками в данной системе координат, то его можно вычислять автоматически по формуле вычисления расстояния между двумя точками (школьный курс геометрии), при этом расстояние для системы координат с числом осей более двух вычисляется аналогично по обобщенной формуле. Собственно совокупность точек графа и будут являться самим графом.
Отмеченные точки графа
Здесь необходимо отмечать те точки графа, которые были пройдены во время работы алгоритма, чтобы не проходить их повторно. Считаю, эти данные должны лежать отдельно от точек графа, потому как такая информация собственно к графу отношения не имеет (а вот к алгоритму самое прямое).
Таблица кратчайших расстояний
Согласно алгоритму изначально расстояние до точек должно представляться максимально возможным расстоянием (за исключением стартовой, до нее расстояние минимально – 0). Затем эти расстояния заполняются в процессе выполнения алгоритма. Также эти расстояния нужны для сравнения имеющихся и предлагаемых расстояний (расстояние до точки 6 для нашего примера).
Маршруты от начальной до остальных точек
Собственно сами маршруты, по которым в дальнейшем будут осуществляться перемещения. Вообще алгоритм Дейкстры не предназначен для поиска маршрутов (только расстояний), но его работа построена таким образом, что формирование маршрута по данному алгоритму не представляет никаких сложностей (в момент оценки и внесения в таблицу кратчайшего расстояния).
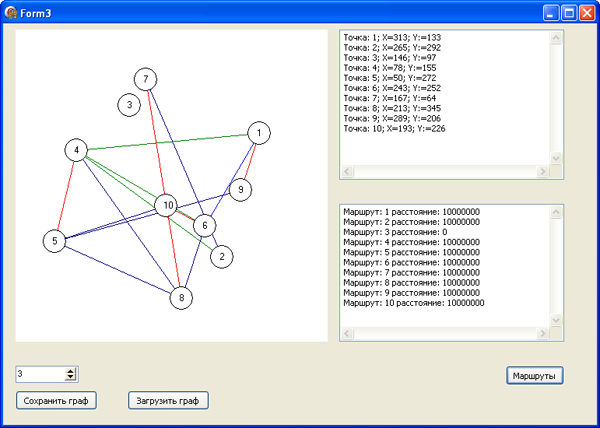
Рис. 2. Тестовая утилита
Заключение
Несмотря на кажущуюся сложность данного алгоритма, при четком понимании работы, его реализация очень проста, а скорость работы вполне приемлема для не очень больших графов.
Исходники тестового проекта прилагаются в виде ресурсов в теме «Журнал клуба программистов. Третий выпуск» или непосредственно в архиве с журналом [5].
Ресурсы
. Реализация алгоритма Дейкстры http://plagiata.net.ru/?p=90
. Описание алгоритма Дейкстры http://algolist.ru/maths/graphs/shortpath/dijkstra.php
. Математическое и неформальное описание алгоритма Дейкстры
http://ru.wikipedia.org/wiki/Алгоритм_Дейкстры
. Дополнительные материалы http://borisvolfson.h11.ru/show_article.php?article_id=0000020 и
http://www.excode.ru/art6837p1.html
. Модули и проекты, использованные в статье http://programmersclub.ru/pro/pro3.zip
Это статья из третьего номера журнала “ПРОграммист”.
Скачать его можно по ссылке.
Ознакомиться со всеми номерами журнала.
17th
Май
 Гауссовское распределение
Гауссовское распределение
К примеру, нормальное (Гауссово) строится используя математическую хитрость о том, что сумма равномерно-распределенных случ. величин – есть нормальная случ. величина.
{ Моделирование нормального распределения }
function Norm: Real;
var
s: Real;
i: Integer;
begin
s := 0;
for i := 1 to Nmax do s := s + Random;
norm := s-Nmax/2;
end;
{ Моделирование распределения скоростей Максвелла }
procedure Maxwell(disp,norm:real;var vx,vy:array of Real);
var
i: integer;
begin
for i := 1 to Nmax do begin
vx := norm*disp;
vy := norm*disp;
end;
end;
Максвеловское (на самом деле это очень похожее на него) приведено для примера. Как управлять дисперсией.
С нормальным немного почесать затылок и можно будет сместить и среднее значение и среднее отклонение.
ЗЫ: Random – встроенный генератор случайных чисел, выдает случайную величину с равномерной плотностью распределения. если что ))
Облако меток
css реестр ассемблер timer SaveToFile ShellExecute программы массив советы word MySQL SQL ListView pos random компоненты дата LoadFromFile form база данных сеть html php RichEdit indy строки Win Api tstringlist Image мысли макросы Edit ListBox office C/C++ memo графика StringGrid canvas поиск файл Pascal форма Файлы интернет Microsoft Office Excel excel winapi журнал ПРОграммист DelphiКупить рекламу на сайте за 1000 руб
пишите сюда - alarforum@yandex.ru
Да и по любым другим вопросам пишите на почту

пеллетные котлы

Пеллетный котел Emtas

Наши форумы по программированию:
- Форум Web программирование (веб)
- Delphi форумы
- Форумы C (Си)
- Форум .NET Frameworks (точка нет фреймворки)
- Форум Java (джава)
- Форум низкоуровневое программирование
- Форум VBA (вба)
- Форум OpenGL
- Форум DirectX
- Форум CAD проектирование
- Форум по операционным системам
- Форум Software (Софт)
- Форум Hardware (Компьютерное железо)


