Введение в SSE

SSE – FPU XXI века

Автор: Ivan32

Аннотация:

В данной статье рассматриваются базовые принципы работы с расширением SSE.

Введение:

С момента создания первого математического сопроцессора(FPU) для х86-процессоров, прошло уже около 30 лет.

Целая эпоха технологий и физических средств их воплощения прошла, с тех пор, и нынешние FPU стали на порядок быстрее, энергоэффективней и компактней того первого FPU – 8087. С тех пор FPU стал частью процессора, что, конечно же, положительно сказалось на его производительности. Тем не менее, нынешняя скорость выполнения команд FPU оставляет желать лучшего.

К счастью это лучшее уже есть. Им стала технология под названием SSE.

Аппаратное введение:

SSE – Streaming SIMD Extensions – был впервые представлен в процессорах серии Pentium III на ядре Katamai.

SIMD – Single Instruction Multiple Data. Аппаратно данное расширение состоит из 8(позже 16, для режима Long Mode-x86-64) и конечно контрольного регистра – MXCSR

В последующих расширениях SSE2 SSE3 SSSE3 SSS4.1 и SSE4.2 только появлялись новые инструкции, в основном нацеленные на специализированные вычисления.

В 2010 появились первые процессоры с поддержкой набора инструкций для аппаратного шифрования AES, этот набор инструкций тоже использует SSE-регистры.

Регистры SSE называются XMM и наличествуют XMM0-XMM7 для 32-битного Protected Mode и дополнительными XMM8-XMM15 для режима 64-битного Long Mode.

Все регистры XMM-регистры 128-битные, но максимальный размер данных, над которым можно совершать операции это FP64-числа. Последнее обусловлено предназначением данного расширения – параллельная обработка данных.

Программное введение:

Когда я только начинал работать с FPU, меня поразила невообразимая сложность работы с ним. Во-первых, из всех 8-ми регистров, прямой доступ был только к двум.

Во-вторых, напрямую загружать данные в них нельзя было, то есть, скажем, инструкция fld 100.0 не поддерживается. А, в-третьих, из регистров общего назначения тоже

нельзя было загрузить данные. Если вторая проблема в SSE не решена, то о первой и третье подобного сказать нельзя.

В данном обзоре рассматриваются только SISD инструкции, призванные заменить FPU аналоги.

Начнем-с. Перво-наперво стоит узнать, как же можно записать данные в xmm-регистр. SSE может работать с FP32 (float) и FP64(double) IEEE754-числами.

Для прямой записи из памяти предусмотрены инструкции MOVSS и MOVSD .

Их мнемоники расшифровываются так:

MOVSS – MOVE SCALAR(Bottom) SINGLE

MOVSD – MOVE SCALAR(Bottom) DOUBLE

Данные инструкции поддерживают только запись вида XMM-to-MEMORY и MEMORY-to-XMM.

Для записи из регистра общего назначения в регистр XMM и обратно есть инструкции MOVD и MOVQ .

Их мнемоники расшифровываются так:

MOVD – MOV DOUBLE WORD(DWORD)

MOVQ – MOV QUAD WORD(QWORD)

Перейдем к основным арифметическим операциям.

Сложение:

ADDSS – ADD SCALAR SINGLE

ADDSD – ADD SCALAR DOUBLE

Вычитание:

SUBSS – SUB SCALAR SINGLE

SUBSD – SUB SCALAR DOUBLE

Умножение:

MULSS – MUL SCALAR SINGLE

MULSD – MUL SCALAR DOUBLE

Деление:

DIVSS – DIV SCALAR SINGLE

DIVSD – DIV SCALAR DOUBLE

Примечание:

XMM-регистры могут быть разделены на два 64-битных FP64 числа или четыре 32-битные FP32 числа.

В данном случае SINGLE и DOUBLE обозначают FP32 и FP64 соответственно. SCALAR – скалярное значение, выраженное одним числом, в отличие от векторного.

В случае работы со скалярными значениями используется нижний SINGLE или DOUBLE(т.е. нижние 32 или 64-бита соответственно) XMM-регистров.

Недостаток SSE заключается в том, что среди инструкций нет тригонометрических функций. Sin Cos Tan Ctan – все эти функции придется реализовать самостоятельно.

Правда, есть бесплатная Intel Aproximated Math Library, скачать ее можно по адресу: www.intel.com/design/pentiumiii/devtools/AMaths.zip.

В связи с данным фактом, в качестве алгоритма для практической реализации был выбран ряд Тейлора для функции синуса. Это ,конечно, не самый быстрый алгоритм,

но, пожалуй, самый простой. Мы будем использовать 8 членов ряда, что предоставит вполне достаточную точность.

В связи со спецификой Protected Mode, а именно, невозможностью прямой передачи 64-битных чисел через стек (нет, конечно, можно, только по частям но неудобно),

рассмотрим еще одну инструкцию, которую мы задействуем в нашей программе.

CVTSS2SD – ConVerT Scalar Single 2(to) Scalar Double

И ее сестра делающая обратное:

СVTSD2SS – ConVerT Scalar Double 2(to) Scalar Single

Данная инструкция принимает два аргумента, в качестве второго аргумента может выступать либо XMM-регистр либо 32-битная ячейка памяти – DWORD.

Примеры использования SSE-комманд:

movss xmm0,dword[myFP32]

movss xmm0,xmm1

movss dword[myFP32],xmm0

movsd xmm0,qword[myFP64]

movsd xmm0,xmm1

movsd qword[myFP64],xmm0

movd xmm0,eax

movd eax,xmm0

add/sub/mul/div:

addss xmm0,dword[myFP32]

subsd xmm0,xmm1

mulss xmm0,dword[myFP32]

divsd xmm0,xmm1

Математическое введение:

В качестве тестового алгоритма мы будем использовать ряд Тейлора для функции синуса. Алгоритм представляет собой простой численный метод.

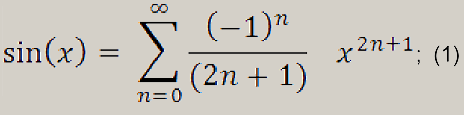
В нашем случае мы используем 8 членов этого ряда, это не слишком много и вполне достаточно для того, что бы обеспечить довольно точные вычисления.

Во всяком случае, отклонение от fsin(аппаратная реализация Sin – FPU) минимально.

Используемая формула выглядит так:

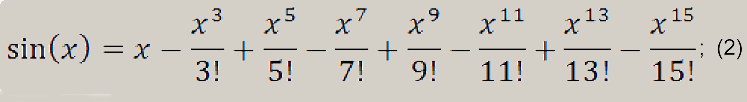
Программная реализация:

В случае с SSE мы воспользуемся всеми восемью регистрами, а что касается FPU – мы будем использовать только st0 и st1.

Благо использование памяти в качестве буфера оказалось эффективней, чем использование всех регистров FPU, к тому же так проще и удобней.

Вычисление будут проходить так:

Сначала мы вычислим значения всех членов ряда, а потом приступим к их суммированию. Подсчет факториалов проводить не будем, так как это пустая

трата процессорного времени в данном случае.

Программная реализация на SSE:

proc sin_sse angle

;Нам понадобятся два экземпляра аргумента:

cvtss2sd xmm0,[angle]     ;; Первый будет выступать как результат возведения в степень.

movq xmm1,xmm0           ;; Второй как множитель, это сделано для того что б минимизировать обращения к памяти.

;; xmm0 = angle.

;; xmm1 = angle. ;; далее x=X=Angle

mulsd xmm0,xmm1 ; Возводим X в третью степень.

mulsd xmm0,xmm1 ;

movq xmm2,xmm0 ; xmm2 = xmm0 = x^3

mulsd xmm0,xmm1 ; Продолжаем возведение.

mulsd xmm0,xmm1 ; Теперь уже в пятую степень.

movq xmm3,xmm0 ; xmm3 = xmm0 = x^5

mulsd xmm0,xmm1

mulsd xmm0,xmm1

movq xmm4,xmm0 ;; xmm4 = xmm0 = x^7

mulsd xmm0,xmm1

mulsd xmm0,xmm1

movq xmm5,xmm0 ;; xmm5 = xmm0 = x^9

mulsd xmm0,xmm1

mulsd xmm0,xmm1

movq xmm6,xmm0 ;; xmm6 = xmm0 = x^11

mulsd xmm0,xmm1

mulsd xmm0,xmm1

movq xmm7,xmm0 ;; xmm7 = xmm0 = x^13

mulsd xmm0,xmm1 ;; Наконец возводим X в 15-ю степень и заканчиваем возведение.

mulsd xmm0,xmm1 ;; xmm0 = x^15

;; Переходим к делению всех промежуточных результатов X ^ n, на n!.

divsd xmm0,[divers_sd+48] ; X^15 div 15!

divsd xmm7,[divers_sd+40] ; X^13 div 13!

divsd xmm6,[divers_sd+32] ; X^11 div 11!

divsd xmm5,[divers_sd+24] ; X^9 div 9!

divsd xmm4,[divers_sd+16] ; X^7 div 7!

divsd xmm3,[divers_sd+8]  ; X^5 div 5!

divsd xmm2,[divers_sd]    ; X^3 div 3!

subsd xmm1,xmm2 ; x – x^3/3!

addsd xmm1,xmm3 ; + x^5 / 5!

subsd xmm1,xmm4 ; – x^7 / 7!

addsd xmm1,xmm5 ; + x^9 / 9!

subsd xmm1,xmm6 ; – x^11 / 11!

addsd xmm1,xmm7 ; + x^13 / 13!

subsd xmm1,xmm0 ; – x^15 / 15!

;; В EAX результат не поместится

movq [SinsdResult],xmm1

;; Но если нужно добавить функции переносимость, есть два варианта.

cvtsd2ss xmm1,xmm1

mov eax,xmm1

ret

SinsdResult dq 0.0

divers_sd dq 6.0,120.0,5040.0,362880.0,39916800.0,6227020800.0,1307674368000.0

endp

Что касается FPU версии данной функции, то в ней мы поступим несколько иначе. Мы воспользуемся буфером в виде 16*4 байт. В последний QWORD

запишем результат. И в качестве делителя будем использовать память, это не страшно т.к. данные будут расположены на одной и той же странице, а это

значит, что данная страница уже будет прокеширована и обращения к ней будут довольно быстрыми. Суммирование и вычитание членов ряда так же будет

проведено в конце.

Программная реализация на FPU:

proc sin_fpu angle

fld [angle]       ; загружаем X. st0=X

fmul [angle]

fmul [angle]      ; st0 = X^3

fld st0           ; st1 = st0

fdiv [divers_fpu] ; Делим X^3 на 3! не отходя от кассы

fstp qword[res]   ; легким движением стека FPU, st1 превращается в st0

;; qword[res] = x^3 / 3!

fmul [angle]

fmul [angle]

fld st0              ; st0 = st1 = X^5

fdiv [divers_fpu+8]

fstp qword[res+8]

;; qword[res+8] = x^5 / 5!

fmul [angle]

fmul [angle]

fld st0              ; st0 = st1 = X^7

fdiv [divers_fpu+16]

fstp qword[res+16]

;; qword[res+16] = x^7 / 7!

fmul [angle]

fmul [angle]

fld st0              ; st0 = st1 = X^9

fdiv [divers_fpu+24]

fstp qword[res+24]

;; qword[res+24] = x^9 / 9!

fmul [angle]

fmul [angle]

fld st0             ; st0 = st1 = X^11

fdiv [divers_fpu+32]

fstp qword[res+32]

;; qword[res+32] = x^11 / 11!

fmul [angle]

fmul [angle]

fld st0             ; st0 = st1 = X^13

fdiv [divers_fpu+40]

fstp qword[res+40]

;; qword[res+40] = x^13 / 13!

fmul [angle]

fmul [angle]        ; st0 = st1 = X^15

fdiv [divers_fpu+48]

fstp qword[res+48]

;; qword[res] = x^15 / 15!

fld [angle]        ; st0 = X

fsub qword[res]    ; X – x^3/3!

fadd qword[res+8]  ; + x^5 / 5!

fsub qword[res+16] ; – x^7 / 7!

fadd qword[res+24] ; + x^9 / 9!

fsub qword[res+32] ; – x^11 / 11!

fadd qword[res+40] ; + x^13 / 13!

fsub qword[res+48] ; – x^15 / 15!

fstp qword[res+56] ; Сохраняем результат вычислений.

ret

res_fpu dq 0.0

res dd 14 dup(0)

divers_fpu dq 6.0,120.0,5040.0,362880.0,39916800.0,6227020800.0,1307674368000.0

endp

Обе функции были протестированы в программе WinTest и вот ее результаты:

sin_FPU – 145-150 тактов в цикле на 1000 итераций и около 1300-1800 при первом вызове при использовании FP64 и 150-165 для FP80.

Такая потеря скорости связана с тем, что при первом вызове память еще не прокеширована.

sin_SSE – около 140-141 тактов в цикле на 1000 итераций, при первом вызове результат аналогичный FPU.

На заметку: так же я тестировал SSE через память (аналогично FPU-алгоритму) и FPU через использование всех регистров, в обоих случаях

имела место серьезная потеря производительности. 220-230 тактов для SSE-версии с использование буферов и около 250-300 для FPU через регистры.

FXCH – оказалась очень медленной инструкцией, а SSE не помогло даже то что страница с данными находилась в кеше.

Примечание:

Основываясь на результатах тестирования, я могу сказать, что разница в результатах может быть лишь погрешностью. Это было проверено опытным путем.

Я несколько раз перезагружал компьютер и в разных случаях выигрывал SSE или FPU. Это дает повод предположить, что имела место немаленькая погрешность

и разница в результатах является ее и только ее порождением. Но Intel Optimization Manual говорит об обратном. По документации разница между SSE и FPU

командами около 1-2 тактов в пользу SSE, т.е. SSE-команды на 1-2 такта в среднем, выполняются быстрее.

Выводы:

Как показала практика, при использовании SSE в качестве FPU мы почти ничего не теряем. Важно то, что такое однопоточное SISD использование не является эффективным.

Всю свою настоящую мощь SSE показывает именно в параллельных вычислениях. Какой смысл считать за N тактов, 1 FP32 сложение/вычитание

или любую другую арифметическую операцию, если можно посчитать за те же N-тактов целых четыре FP32 или 2 FP64. Вопрос остается лишь

в распараллеливании алгоритмов. Стоит ли использовать SSE? Однозначно стоит. Данное расширение присутствует во всех процессорах, начиная с Pentium III и AMD K7.

Важно: Регистры XMM предположительно не сохраняються при переключении задач и точно не сохраняются при использовании API. Тот же GDI+ не восстанавливает их значения.

Nota Bene:

1. Тестирование проводилось на процессоре с не самым старым ядром. Еще при релизе мелькала фраза о масштабных оптимизациях во всех блоках.

При схожей частоте данный процессор в ряде приложений оказывается быстрее, чем, скажем Core 2 на ядре Conroe(первое поколение Core 2).

Это собственно к чему: SSE не всегда было таким быстрым, как и FPU. На разных архитектурах вы увидите как выигрыш от использования SSE

так и серьезный проигрыш.

2. Данный численный метод не является самым быстрым, он даже не распараллелен. Аппаратный FSIN выполняется за 80-100 тактов с FP80/FP64 точностью.

Существуют так же другие численные методы для нахождения тригонометрических и других функций, которые намного эффективней данного и практически позволяют

сделать эти вычисления более быстрыми, нежели FSIN.

Програмно-аппаратная конфигурация:

CPU: Intel Core 2 Duo E8200 2.66 Ghz @ 3.6 Ghz 450.0 FSB * 8.0.

RAM: Corsair XMS2 5-5-5-18 800Mhz @ 900Mhz 5-6-6-21. FSB:MEM = 1:2

MB:  Gigabyte GA P35DS3L (BIOS неизвестен – никогда не изменялся.)

GPU: Saphire Radeon HD5870 1GB GPU Clock = 850 Mhz Memory Clock = 4800(1200 Phys).

PSU: Cooler Master Elite 333 Stock PSU 450 Wt.

OS: Windows 7 Ultimate x86

FASM: 1.67 recompiled by MadMatt(Matt Childress).

Ссылки:

http://users.egl.net/talktomatt/default.html

http://programmersforum.ru/showthread.php?t=55270 – тема, где можно найти программу для тестирования времени выполнения.

Автор данной программы некто bogrus. Его профиль есть на форуме WASM.RU но, он неактивен уже 3-й год.

Статья из второго выпуска “журнала ПРОграммистов”.
Скачать этот номер можно по ссылке.
Ознакомиться со всеми номерами журнала.

Обсудить на форуме — Введение в SSE